icodepro.ruУсловие задачи:
Человек массой 80 кг захотел спуститься по веревочной лестнице из свободно висящего на высоте 15 м аэростата массой 400 кг. Какой минимальной длины лестницу надо привязать к аэростату, чтобы последняя ступенька коснулась земли, когда на неё встанет человек?
Задача №2.10.31 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=80\) кг, \(H=15\) м, \(M=400\) кг, \(L-?\)
Решение задачи:
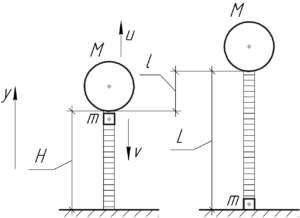Рассмотрим систему “аэростат – человек”. Так как аэростат свободно висит на некоторой высоте, значит по первому закону Ньютона действие внешних сил на систему скомпенсировано. Если изначально аэростат с человеком не двигались, то есть суммарный импульс равен нулю, значит и после того, как человек начнет движение по лестнице, суммарный импульс останется таким же по закону сохранения импульса в проекции на ось \(y\):
\[0 = – m\left( {\upsilon – u} \right) + Mu\]
Внимание! Все импульсы (скорости) должны быть записаны относительно одной системы отсчета – в данном случае относительно Земли. Человек спускается со скоростью \(\upsilon\) относительно лестницы (то есть аэростата), а аэростат начинает подниматься со скоростью \(u\), значит его скорость относительно Земли равна \(– \left( {\upsilon – u} \right)\).
Преобразуем полученное равенство:
\[m\left( {\upsilon – u} \right) = Mu\]
\[m\upsilon – mu = Mu\]
\[m\upsilon = \left( {M + m} \right)u\]
Человек будет опускаться то же время, что и аэростат подниматься. При этом человек пройдет расстояние \(L\), а аэростат поднимется на высоту \(l\), равную \(\left( {L – H} \right)\). Будет правильно записать такую систему:
\[\left\{ \begin{gathered}
\upsilon = \frac{L}{t} \hfill \\
u = \frac{l}{t} = \frac{{L – H}}{t} \hfill \\
\end{gathered} \right.\]
Тогда:
\[m\frac{L}{t} = \left( {M + m} \right)\frac{{L – H}}{t}\]
\[mL = \left( {M + m} \right)\left( {L – H} \right)\]
Раскроем скобки и найдем искомую длину лестницы \(L\).
\[mL = ML – MH + mL – mH\]
\[ML = \left( {m + M} \right)H\]
\[L = \frac{{\left( {m + M} \right)H}}{M}\]
Посчитаем ответ, подставив исходные данные в формулу:
\[L = \frac{{\left( {80 + 400} \right) \cdot 15}}{{400}} = 18\; м\]
Эту задачу также можно решать, используя теорему о движении центра масс.
Ответ: 18 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.30 Тележка стоит на гладких рельсах. Человек переходит с одного её конца на другой
2.10.32 Два шарика массами 2 и 3 г движутся в горизонтальной плоскости со скоростями
2.10.33 Космический корабль на скорости 10 км/с попадает в неподвижное облако
Спорить не буду, но, похоже, обычному школьнику вообще мало что известно… И авторам учебников тоже. Например, Пёрышкин после параграфа о массе, совершенно спокойно даёт пару задач на закон сохранения импульса задолго до темы “динамика”.
Если нет центра масс, то не очень понятно, как разделять движение под действием силы на вращательное и поступательное…
Но вообще после заявлений, что “обычному школьнику…” я начинаю задумываться – а откуда я это вообще взял и после размышлений обычно получается, что всё-таки где-то в школе.
Явно там где-то возле вывода закона сохранения импульса из третьего закона Ньютона и материальной точки должен быть центр масс из второго…
Хорошо, про потенциальную энергию школьник же должен знать? Полагая, что человек коснулся земли с нулевой скоростью и, считая нулём потенциальной энергии землю, запишем закон сохранения энергии:
(M+m)*g*H = M*g*L + 0.
В школе обычно дают что такое центр масс, но не дают теорему о движении центра масс. Не буду спорить – школы тоже бывают разные.
Решение с законом сохранения энергии, который Вы привели, считаю самым простым и наиболее рациональным в данной задаче. Спасибо Вам!
Это честный, но безумно не рациональный способ.
“Так как аэростат свободно висит на некоторой высоте, значит по первому закону Ньютона действие внешних сил на систему скомпенсировано.”(с) Следовательно центр масс системы, состоящей из аэростата и человека неподвижен.
Пусть L – длина лестницы (она же высота аэростата в момент когда человек коснётся земли), М и m – массы аэростата и человека, H – положение центра масс (исходная высота аэростата). В системе отсчёта связанной с землёй положение центра масс:
H = M*L/(M+m).
Я пошёл сложным путем, это Вы заметили верно.
Но я решил задачу в рамках школьного курса, Вы же используете теорему о движении центра масс (вернее её следствие), которая обычному школьнику неизвестна.