Через неподвижный блок перекинута нить, к концам которой подвешены грузы

Условие задачи:

Через неподвижный блок перекинута нить, к концам которой подвешены грузы массой 3 и 1,9 кг. Найти силу натяжения нити. Считать, что трение в блоке отсутствует. Массой нити и блока пренебречь.

Задача №2.2.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(M=3\) кг, \(m=1,9\) кг, \(T-?\)

Решение задачи:

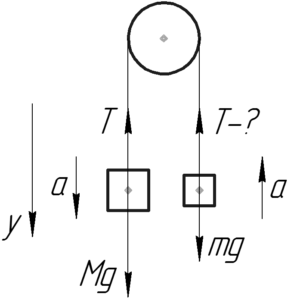Изобразим схему и покажем все силы, которые действуют на грузы. Очевидно, что груз \(M\) перетянет груз \(m\), значит движение будет происходить в сторону большего груза. Ускорение грузов одинаково, так как она нерастяжима.

Запишем второй закон Ньютона в проекции на ось \(y\) для обоих грузов:

\[\left\{ \begin{gathered}
Mg – T = Ma \hfill \\
mg – T = – ma \hfill \\
\end{gathered} \right.\]

В этой системе два неизвестных. Чтобы избавиться от неизвестного ускорения \(a\), поделим верхнее равенство на нижнее, тогда получим:

\[\frac{{Mg – T}}{{mg – T}} = \frac{M}{{ – m}}\]

Перемножим “крест-накрест”, тогда:

\[ – Mmg + Tm = Mmg – TM\]

\[T\left( {M + m} \right) = 2Mmg\]

\[T = \frac{{2Mmg}}{{M + m}}\]

Посчитаем ответ:

\[T = \frac{{2 \cdot 3 \cdot 1,9 \cdot 10}}{{3 + 1,9}} = 23,27\; Н\]

Ответ: 23,27 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.2.2 Три груза массами m1=1 кг, m2=2 кг, m3=3 кг соединены легкими нитями, проходящими
2.2.4 Два грузика массами m1=0,3 кг и m2=0,2 кг соединены нитью, перекинутой через блок
2.2.5 Два одинаковых груза массами 0,1 кг связаны между собой нитью, перекинутой