Условие задачи:

Для откачки воды из шахты глубиной 20 м поставлен насос с двигателем мощностью 4,5 кВт. Сколько кубометров воды можно поднять из шахты за 7 ч работы насоса, если КПД двигателя 80%?

Задача №2.8.27 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$h=20$ м, $N=4,5$ кВт, $t=7$ ч, $\eta=80$%, $V-?$

Решение задачи:

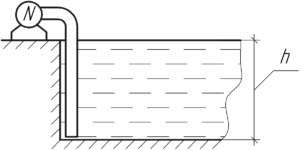Так как в задаче идет речь об КПД двигателя насоса, то запишем формулу для определения КПД (в долях единицы):

$$\eta  = \frac{{{A_п}}}{{{A_з}}}\;\;\;\;(1)$$

В этой формуле $A_п$ — полезная работа двигателя, $A_з$ — затраченная работа двигателя. Полезная работа двигателя заключается в увеличении потенциальной энергии воды:

$${A_п} = mgh$$

Здесь нужно сделать пояснение — конец всасывающего шланга насоса располагается как раз на глубине, равной глубине шахты, то есть на дне. Поэтому каждая откачанная часть воды $\Delta m$ обязательно пройдет по вертикали расстояние $h$, изменив свою потенциальную энергию на величину $\Delta mgh$. А значит и вся откачанная масса воды $m$ изменит свою потенциальную энергию на величину $mgh$. В этой задаче нельзя рассматривать объем воды через его центр масс.

Масса воды связана с объемом через плотность по формуле:

$$m = \rho V$$

Напомним, что плотность воды равна $\rho=1000\; кг/м^3$.

Тогда выражение для полезной работы примет вид:

$${A_п} = \rho Vgh\;\;\;\;(2)$$

Затраченную работу определим через формулу мощности двигателя насоса:

$$N = \frac{{{A_з}}}{t}$$

$${A_з} = Nt\;\;\;\;(3)$$

Подставим выражения (2) и (3) в (1), из получившейся формулы выразим искомый объем воды $V$.

$$\eta  = \frac{{\rho Vgh}}{{Nt}}$$

$$V = \frac{{\eta Nt}}{{\rho gh}}$$

Время в формулу нужно подставлять в секундах, а КПД — в долях единицы. Покажем перевод этих единиц в систему СИ.

$$7\; ч = 7 \cdot 3600\; с = 25200\; с$$

$$80% = 0,8$$

Только теперь, подставив значения в формулу, посчитаем ответ.

$$V = \frac{{0,8 \cdot 4,5 \cdot {{10}^3} \cdot 25200}}{{1000 \cdot 10 \cdot 20}} = 453,6\; м^3$$

Ответ: 453,6 м³.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.26 Пуля, летящая горизонтально со скоростью 510 м/с, попадает в ящик, лежащий
2.8.28 Какую работу надо совершить, чтобы поставить однородный куб массой 10 кг
2.8.29 Камень бросили под углом 60 градусов к горизонту со скоростью 15 м/с. Найдите