Решение: Допустим, что сила, которая заставляет баржу двигаться по каналу, прямо пропорциональна

Условие задачи:

Допустим, что сила, которая заставляет баржу двигаться по каналу, прямо пропорциональна скорости. Чтобы баржа двигалась со скоростью 2 км/ч, необходима мощность 4 кВт. Какая требуется мощность, чтобы баржа двигалась со скоростью 6 км/ч?

Задача №2.7.48 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$F=k \upsilon$ , $\upsilon_1=2$ км/ч, $N_1=4$ кВт, $\upsilon_2=6$ км/ч, $N_2-?$

Решение задачи:

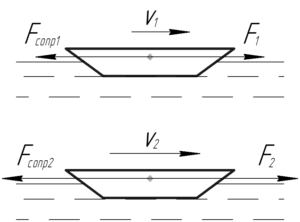Почему сила, которая заставляет баржу двигаться по каналу, то есть сила тяги баржи, прямо пропорциональна скорости? Дело в том, что при равномерном движении сила тяги баржи должна быть равна силе сопротивлению воды по первому закону Ньютона.

$F = {F_{сопр}}$

Последняя (сила сопротивления $F_{сопр}$ ) — прямо пропорциональна скорости баржи.

${F_{сопр}} = k\upsilon \Rightarrow F = k\upsilon$

При равномерном движении мощность баржи $N$ определяется по такой формуле:

$N = F \cdot \upsilon$

Учитывая, что $F=k \upsilon$ , имеем:

$N = k{\upsilon ^2}$

Здесь $k$ — некий коэффициент (не зависящий от скорости и мощности), значение которого не понадобится при решении этой задачи.

Запишем последнюю формулу для двух случаев, о которых говорится в условии.

$\left\{ \begin{gathered} {N_1} = k\upsilon _1^2 \hfill \\ {N_2} = k\upsilon _2^2 \hfill \\ \end{gathered} \right.$

Поделим нижнее равенство на верхнее:

$\frac{{{N_2}}}{{{N_1}}} = \frac{{\upsilon _2^2}}{{\upsilon _1^2}}$

${N_2} = {N_1}\frac{{\upsilon _2^2}}{{\upsilon _1^2}}$

По этой формуле уже можно считать ответ. Переводить скорости в систему СИ не имеет смысла, поскольку в формуле фигурирует отношение скоростей, которое не зависит от единицы измерения.

${N_2} = 4000 \cdot \frac{{{6^2}}}{{{2^2}}} = 36000\;Вт = 36\;кВт$