Два автомобиля массами m и 2m движутся в одном направлении с одинаковыми

Условие задачи:

Два автомобиля массами m и 2m движутся в одном направлении с одинаковыми скоростями v. Чему равен модуль импульса второго автомобиля в системе отсчета, связанной с первым автомобилем?

Задача №2.1.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m\), \(2m\), \(\upsilon\), \(p_{21}-?\)

Решение задачи:

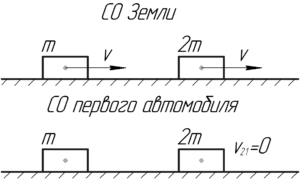Перейдем в системе отсчета (СО), связанную с первым автомобилем. Чтобы узнать скорость второго автомобиля в этой СО, нужно к вектору его скорости прибавить вектор, равный по величине и противоположный по направлению вектору первого автомобиля. Так как скорости обоих автомобилей равны и сонаправлены (в СО Земли), значит второй автомобиль имеет нулевую скорость в СО первого.

\[{\upsilon _{21}} = 0\]

Значит и его импульс в этой СО равен нулю.

\[{p_{21}} = m{\upsilon _{21}}\]

\[{p_{21}} = 0\]

Ответ: 0 кг·м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.1.25 Скорость автомобиля изменяется по закону v=10+0,5t. Найдите результирующую
2.1.27 Пуля массой 10 г, летевшая со скоростью 400 м/с, пробив доску толщиной 5 см
2.1.28 Пуля массой 9 г, летевшая со скоростью 600 м/с, попадает в деревянную стену