Гирька массой 0,05 кг, привязанная к нити длиной 0,26 м, описывает в горизонтальной

Условие задачи:

Гирька массой 0,05 кг, привязанная к нити длиной 0,26 м, описывает в горизонтальной плоскости окружность. Каким должен быть период вращения, чтобы сила натяжения нити не превышала 1,96 Н?

Задача №2.4.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=0,05\) кг, \(L=0,26\) м, \({T_н} \leq 1,96\) Н, \(T-?\)

Решение задачи:

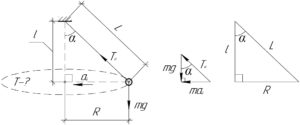На гирьку действуют две силы: сила тяжести \(mg\) и сила натяжения \(T_н\), над действием которых гирька совершает в горизонтальной плоскости движение по окружности с некоторым радиусом \(R\) и центростремительным ускорением \(a_ц\), при этом нить составляет с вертикалью некоторый угол \(\alpha\) (смотрите схему).

Рассмотрим векторный треугольник, получившийся при сложении всех действующих на гирьку сил (опять посмотрите схему). Понятно, что этот треугольник – прямоугольный, поэтому согласно теореме Пифагора справедливо следующее равенство:

\[T_н^2 = {m^2}a_ц^2 + {m^2}{g^2}\;\;\;\;(1)\]

Отлично, теперь из этого же векторного треугольника получим выражение для нахождения тангенса угла \(\alpha\):

\[tg\alpha = \frac{{m{a_ц}}}{{mg}}\]

\[tg\alpha = \frac{{{a_ц}}}{g}\;\;\;\;(2)\]

Как было уже сказано, гирька, подвешенная на нити длиной \(L\), движется по окружности с некоторым радиусом \(R\), при этом нить составляет с вертикалью некоторый угол \(\alpha\). Пусть \(l\) – расстояние от точки подвеса нити до плоскости вращения гирьки. Рассмотрим ещё один прямоугольный треугольник (смотрите схему), из которого также найдём выражение для тангенса угла \(\alpha\):

\[tg\alpha = \frac{R}{l}\]

Расстояние \(l\) найдём, применив второй раз теорему Пифагора:

\[l = \sqrt {{L^2} – {R^2}} \]

Тогда:

\[tg\alpha = \frac{R}{{\sqrt {{L^2} – {R^2}} }}\;\;\;\;(3)\]

Приравняем (2) и (3):

\[\frac{{{a_ц}}}{g} = \frac{R}{{\sqrt {{L^2} – {R^2}} }}\]

Возведём обе части в квадрат и выразим из получившегося равенства \(g^2\):

\[\frac{{a_ц^2}}{{{g^2}}} = \frac{{{R^2}}}{{{L^2} – {R^2}}}\]

\[{g^2} = a_ц^2\frac{{{L^2} – {R^2}}}{{{R^2}}}\]

Полученное подставим в (1):

\[T_н^2 = {m^2}a_ц^2 + {m^2}a_ц^2\frac{{{L^2} – {R^2}}}{{{R^2}}}\]

\[T_н^2 = {m^2}a_ц^2\frac{{{L^2}}}{{{R^2}}}\]

\[{T_н} = m{a_ц}\frac{L}{R}\;\;\;\;(4)\]

Формулу для определения центростремительного ускорения гирьки запишем через угловую скорость вращения \(\omega\):

\[{a_ц} = {\omega ^2}R\;\;\;\;(5)\]

Формула связи угловой скорости и периода вращения выглядит так:

\[\omega  = \frac{{2\pi }}{T}\;\;\;\;(6)\]

Подставим выражение (6) в формулу (5), тогда:

\[{a_ц} = \frac{{4{\pi ^2}R}}{{{T^2}}}\]

Полученное подставим в (4), в итоге:

\[{T_н} = \frac{{4{\pi ^2}mL}}{{{T^2}}}\]

Задача почти решена, осталось совсем немного. В задаче дано условие, что \({T_н} \leq {T_{нм}}\), где \({T_{нм}}\) – максимальная сила натяжения нити, равная 1,96 Н. Мы получим такую систему:

\[\left\{ \begin{gathered}
{T_н} = \frac{{4{\pi ^2}mL}}{{{T^2}}} \hfill \\
{T_н} \leq {T_{нм}} \hfill \\
\end{gathered} \right.\]

Откуда:

\[{T_{нм}} \geq \frac{{4{\pi ^2}mL}}{{{T^2}}}\]

\[{T^2} \geq \frac{{4{\pi ^2}mL}}{{{T_{нм}}}}\]

\[T \geq \sqrt {\frac{{4{\pi ^2}mL}}{{{T_{нм}}}}} \]

\[T \geq 2\pi \sqrt {\frac{{mL}}{{{T_{нм}}}}} \]

Минимальный период вращения, при котором сила натяжения не будет превышать \({T_{нм}}\), соответствует случаю равенства:

\[T = 2\pi \sqrt {\frac{{mL}}{{{T_{нм}}}}} \]

Подставим данные задачи и посчитаем ответ:

\[T = 2 \cdot 3,14 \cdot \sqrt {\frac{{0,05 \cdot 0,26}}{{1,96}}}  = 0,51\; с\]

Ответ: 0,51 с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.3 Автомобиль массой 5 т движется с постоянной по модулю скоростью 10 м/с
2.4.5 Гиря массой 100 г равномерно вращается на нити в вертикальной плоскости
2.4.6 Горизонтально расположенный диск равномерно вращается вокруг вертикальной оси