Решение: Гиря массой 100 г равномерно вращается на нити в вертикальной плоскости. На

Условие задачи:

Гиря массой 100 г равномерно вращается на нити в вертикальной плоскости. На сколько сила натяжения нити при прохождении гири через нижнюю точку больше, чем через верхнюю?

Задача №2.4.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=100\) г, \(\Delta T-?\)

Решение задачи:

Искомое значение \(\Delta T\) – это разность сил натяжения нити в нижней и верхней точке:

\[\Delta T = {T_н} – {T_в}\;\;\;\;(1)\]

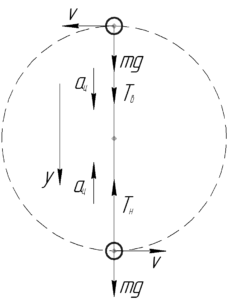
На схеме изобразим эти два положения гири и покажем все силы, действующие на неё. Запишем второй закон Ньютона в проекции на ось \(y\) для обоих положений:

\[\left\{ \begin{gathered}
mg + {T_в} = m{a_ц} \hfill \\
mg – {T_н} = – m{a_ц} \hfill \\
\end{gathered} \right.\]

Прошу заметить, что центростремительное ускорение гири везде одинаковое, так как движение гири по окружности равномерное (т.е. с одной и той же скоростью).

Поделим верхнее равенство системы на нижнее, тогда:

\[\frac{{mg + {T_в}}}{{mg – {T_н}}} = – 1\]

\[mg + {T_в} = – mg + {T_н}\]

\[{T_н} – {T_в} = 2mg\]

Учитывая последнее, равенство (1) примет вид:

\[\Delta T = 2mg\]

Переведем массу гири в систему СИ:

\[100\; г = \frac{{100}}{{1000}}\; кг = 0,1\; кг\]

Посчитаем ответ:

\[\Delta T = 2 \cdot 0,1 \cdot 10 = 2\; Н\]