Из орудия вылетает снаряд массой 10 кг со скоростью 500 м/с. Найти силу давления

Условие задачи:

Из орудия вылетает снаряд массой 10 кг со скоростью 500 м/с. Найти силу давления пороховых газов, считая её постоянной во все время движения снаряда внутри ствола орудия, равное 0,01 с.

Задача №2.1.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=10\) кг, \(\upsilon=500\) м/с, \(\Delta t=0,01\) с, \(F-?\)

Решение задачи:

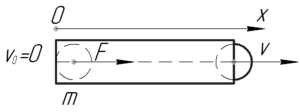Сила давления пороховых газов найдем согласно второму закону Ньютона, записанного в общем виде:

\[F = \frac{{\Delta p}}{{\Delta t}}\;\;\;\;(1)\]

В этой формуле \({\Delta p}\) – это модуль изменения импульса снаряда. Так как в момент выстрела из пушки скорость снаряда была равна нулю (значит и импульс нуль), то очевидно, что модуль изменения импульса равен конечному импульсу снаряда при вылете из ствола.

\[\Delta p = m\upsilon \;\;\;\;(2)\]

Подставив выражение (2) в (1), получим ответ к задаче в общем виде.

\[F = \frac{{m\upsilon }}{{\Delta t}}\]

Посчитаем ответ, подставив численные данные задачи в полученную формулу.

\[F = \frac{{10 \cdot 500}}{{0,01}} = 5 \cdot {10^5}\; Н = 500\; кН\]

Ответ: 500 кН.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.1.23 Тело массой 50 г, падающее со скоростью 2 м/с, упруго соударяется с горизонтальной
2.1.25 Скорость автомобиля изменяется по закону v=10+0,5t. Найдите результирующую
2.1.26 Два автомобиля массами m и 2m движутся в одном направлении с одинаковыми