К вертикальной стенке с силой 40 Н, направленной горизонтально, прижимается брусок

Условие задачи:

К вертикальной стенке с силой 40 Н, направленной горизонтально, прижимается брусок массой 4 кг. Определить модуль импульса бруска через 1,5 с с момента начала движения, если коэффициент трения бруска о стену равен 0,1.

Задача №2.1.72 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(F=40\) Н, \(m=4\) кг, \(t=1,5\) с, \(\mu=0,1\), \(p-?\)

Решение задачи:

Модуль импульса бруска \(p\) через время \(t\) найдём по формуле:

\[p = m\upsilon \]

Брусок будет двигаться вниз с некоторым ускорением \(a\) из состояния покоя, поэтому верна формула скорости для равноускоренного движения без начальной скорости:

\[\upsilon  = at\]

\[p = mat\;\;\;\;(1)\]

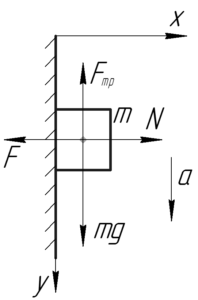
Получается, чтобы найти ответ к задаче, нужно определить ускорение бруска \(a\). На схеме нарисуем брусок и покажем все действующие на него силы. Запишем законы Ньютона в проекции на оси координат:

\[\left\{ \begin{gathered}
ox:N = F \;\;\;\;(2)\hfill \\
oy:mg – {F_{тр}} = ma \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]

Сила трения скольжения определяется по формуле (исходя из равенства (2)):

\[{F_{тр}} = \mu N = \mu F\]

Таким образом:

\[mg – \mu F = ma\]

\[a = \frac{{mg – \mu F}}{m}\]

Подставим полученное выражение в формулу (1).

\[p = m\frac{{mg – \mu F}}{m}t = \left( {mg – \mu F} \right)t\]

Подставим данные задачи и посчитаем ответ.

\[p = \left( {4 \cdot 10 – 0,1 \cdot 40} \right) \cdot 1,5 = 54\; кг \cdot м/с\]

Ответ: 54 кг·м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.1.71 Есть два способа закинуть льдинку: бросить её под углом 45 градусов к горизонту или
2.1.73 На гладкой поверхности лежит доска массой 5 кг, на ней находится тело массой 3 кг
2.1.74 Струя сечением 6 см2 ударяет из брандспойта в стенку под углом 60 градусов к нормали