Какую минимальную работу необходимо совершить, чтобы передвинуть по

Условие задачи:

Какую минимальную работу необходимо совершить, чтобы передвинуть по горизонтальной плоскости груз массой 10 кг на расстояние 1 м с помощью невесомого резинового упругого жгута с жесткостью 10 Н/м. Жгут тянут горизонтально, в начальный момент он не растянут. Коэффициент трения груза о плоскость равен 0,1.

Задача №2.6.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=10\) кг, \(S=1\) м, \(k=10\) Н/м, \(\mu=0,1\), \(A-?\)

Решение задачи:

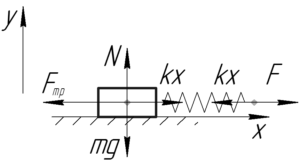Чтобы передвинуть груз, нужно приложить некоторую силу \(F\) к жгуту, работу \(A\) которой и нужно найти. Интересно, что пока сила упругости \(kx\) не станет равна максимальной силе трения покоя (равной силе трения скольжения), груз будет оставаться в покое. Т.е. в момент трогания груза жгут будет растянут на некоторую величину \(x\). Для того, чтобы найти эту величину, запишем первый закон Ньютона:

\[kx = {F_{тр}}\]

Максимальная сила трения покоя равна (учитывая, что \(N=mg\) по первому закону Ньютона):

\[{F_{тр}} = \mu N = \mu mg\;\;\;\;(1)\]

Тогда:

\[kx = \mu mg\]

\[x = \frac{{\mu mg}}{k}\;\;\;\;(2)\]

Далее груз тянут с некоторой очень маленькой скоростью \(\upsilon\), чтобы совершаемая работа была минимальной.

Чтобы найти искомую работу \(A\), запишем закон сохранения энергии. При этом стоит отметить, что на систему “груз-жгут” действует внешняя сила \(F\) и неконсервативная сила \(F_{тр}\). Эти обе силы совершают работу (сила трения – отрицательную), а пружина увеличивает свою потенциальную энергию.

\[A – {F_{тр}} \cdot S = \frac{{k{x^2}}}{2}\]

\[A = {F_{тр}} \cdot S + \frac{{k{x^2}}}{2}\]

Учитывая ранее полученные выражения (1) и (2), имеем:

\[A = \mu mgS + \frac{k}{2} \cdot \frac{{{\mu ^2}{m^2}{g^2}}}{{{k^2}}}\]

\[A = \mu mg\left( {S + \frac{{\mu mg}}{{2k}}} \right)\]

Получено решение задачи в общем виде. Посчитаем ответ:

\[A = 0,1 \cdot 10 \cdot 10 \cdot \left( {1 + \frac{{0,1 \cdot 10 \cdot 10}}{{2 \cdot 10}}} \right) = 15\;Дж\]

Ответ: 15 Дж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.6.13 Груз массой 4 кг подвешен на пружине жесткостью 1 кН/м. Определите дополнительную
2.6.15 Деревянный брусок массы 2 кг тянут равномерно по горизонтальной доске с помощью
2.7.1 Какую работу надо совершить, чтобы растянуть пружину с жесткостью 40 кН/м