Решение: Камень массой 100 г бросили под углом 60 градусов к горизонту со скоростью 15 м/с

Условие задачи:

Камень массой 100 г бросили под углом 60° к горизонту со скоростью 15 м/с. Найдите потенциальную энергию камня спустя 1 с после начала движения.

Задача №2.7.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

\(m=100\) г, \(\alpha=60^\circ\), \(\upsilon_0=15\) м/с, \(t=1\) с, \(E_п-?\)

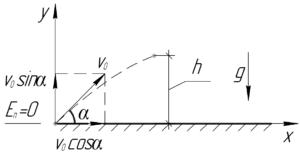Если принять за уровень отсчета потенциальной энергии уровень поверхности земли, то искомую потенциальную энергию \(E_п\) легко найдем по формуле:

\[{E_п} = mgh\;\;\;\;(1)\]

Чтобы найти высоту \(h\), на которую поднимется камень через \(t\) секунд, запишем уравнение движения камня в проекции на ось \(y\):

\[h = {\upsilon _0}\sin \alpha \cdot t – \frac{{g{t^2}}}{2}\]

Подставим полученное выражение в (1):

\[{E_п} = mg\left( {{\upsilon _0}\sin \alpha \cdot t – \frac{{g{t^2}}}{2}} \right)\]

Переведем массу камня в килограммы и произведем вычисление ответа.

\[100\;г = \frac{{100}}{{1000}}\;кг = 0,1\;кг\]

\[{E_п} = 0,1 \cdot 10 \cdot \left( {15 \cdot \sin 60^\circ \cdot 1 – \frac{{10 \cdot {1^2}}}{2}} \right) = 8\;Дж\]

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.