Условие задачи:
Канат лежит на плоской горизонтальной крыше так, что часть его свешивается с крыши. Определить коэффициент трения каната о крышу, если канат начинает скользить вниз, когда 0,15 его длины свешивается с крыши.
Задача №2.1.63 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=0,15\), \(\mu-?\)
Решение задачи:
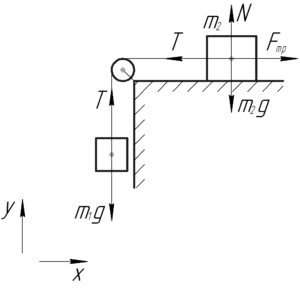 Чтобы решить эту задачу нужно нарисовать эквивалентную схему, которую вы можете видеть на рисунке.
Чтобы решить эту задачу нужно нарисовать эквивалентную схему, которую вы можете видеть на рисунке.
На самом столе лежит брусок массой \(m_2=\left( {1 — \alpha } \right)m\), который олицетворяет часть каната, лежащего на столе, и соединяется с висящим бруском массой \(m_1=\alpha m\) через неподвижный блок — это замена части каната, свисающего с крыши.
Так как нас интересует случай, когда канат только начинает соскальзывать с крыши, то запишем первый закон Ньютона для обоих брусков.
Для висящего бруска:
\[oy:\alpha mg — T = 0\;\;\;\;(1)\]
Для бруска, лежащего на столе:
\[\left\{ \begin{gathered}
ox:T — {F_{тр}} = 0 \;\;\;\;(2)\hfill \\
oy:N = \left( {1 — \alpha } \right)mg \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]
Силу трения скольжения определяют по формуле:
\[{F_{тр}} = \mu N\]
Учитывая выражение (3), формула примет вид:
\[{F_{тр}} = \mu \left( {1 — \alpha } \right)mg\]
Сложим вместе выражения (1) и (2), и в полученную формулу подставим выражение, определяющее силу трения.
\[\alpha mg — {F_{тр}} = 0\]
\[\alpha mg — \mu \left( {1 — \alpha } \right)mg = 0\]
\[\mu = \frac{\alpha }{{1 — \alpha }}\]
Посчитаем численное значение коэффициента трения.
\[\mu = \frac{{0,15}}{{1 — 0,15}} = \frac{3}{{17}} = 0,18\]
Ответ: 0,18.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.62 Материальная точка массой 1 кг движется со скоростью, которая изменяется по закону
2.1.64 Мяч массой 0,2 кг движется к стене под углом 30 градусов к ней со скоростью 6 м/с
2.1.65 Пуля массой 0,3 г, выпущенная из пневматической винтовки вертикально вверх, упала

 icodepro.ru
icodepro.ru