Решение: Мальчик, стоя на Земле, бросает камень горизонтально со скоростью 5 м/с

Условие задачи:

Мальчик, стоя на Земле, бросает камень горизонтально со скоростью 5 м/с. Какую скорость он может сообщить камню, совершая при броске ту же работу, стоя на гладком льду? Масса мальчика 49 кг, камня – 1 кг.

Задача №2.10.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_0=5\) м/с, \(M=49\) кг, \(m=1\) кг, \(\upsilon-?\)

Решение задачи:

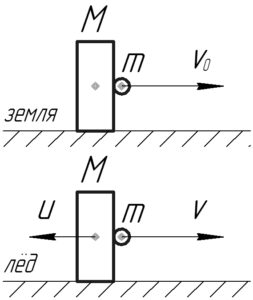Стоя на земле, мальчик сообщает скорость \(\upsilon_0\) камню (кинетическую энергию), вследствие чего он совершает работу, равную:

\[A = \frac{{m\upsilon _0^2}}{2}\;\;\;\;(1)\]

Если ж мальчик будет стоять на льду, то при броске он сам не сможет оставаться неподвижным, т.е. сообщая скорость \(\upsilon\) камню, он и сам приобретет скорость \(u\). Тогда работа мальчика будет равна:

\[A = \frac{{m{\upsilon ^2}}}{2} + \frac{{M{u^2}}}{2}\;\;\;\;(2)\]

Обратите внимание, что \(\upsilon < {\upsilon _0}\).

Запишем закон сохранения импульса для этого случая, откуда найдем скорость отката \(u\) мальчика:

\[0 = m\upsilon – Mu\]

\[u = \frac{{m\upsilon }}{M}\;\;\;\;(3)\]

Подставим выражение (3) в формулу (2):

\[A = \frac{{m{\upsilon ^2}}}{2} + \frac{M}{2} \cdot \frac{{{m^2}{\upsilon ^2}}}{{{M^2}}} = \frac{{m{\upsilon ^2}}}{2} + \frac{{{m^2}{\upsilon ^2}}}{{2M}}\]

\[A = \frac{{m{\upsilon ^2}\left( {M + m} \right)}}{{2M}}\;\;\;\;(4)\]

Так как работы в обоих случаях равны, то можем приравнять (1) и (4):

\[\frac{{m\upsilon _0^2}}{2} = \frac{{m{\upsilon ^2}\left( {M + m} \right)}}{{2M}}\]

\[{\upsilon ^2} = \frac{{\upsilon _0^2M}}{{M + m}}\]

\[\upsilon = {\upsilon _0}\sqrt {\frac{M}{{M + m}}} \]

Посчитаем ответ:

\[\upsilon = 5\sqrt {\frac{{49}}{{49 + 1}}} = 4,95\; м/с = 17,82\; км/ч\]