Решение: На рисунке приведена зависимость потенциальной энергии от времени движения

Условие задачи:

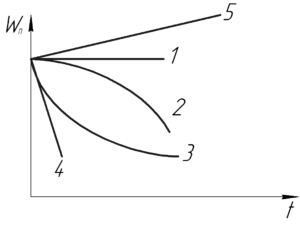На рисунке приведена зависимость потенциальной энергии от времени движения. Для какого из движений сила имеет минимальное значение?

Задача №2.7.41 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

Не совсем понятно какую силу имел в виду автор, поэтому мы будем думать, что всё-таки равнодействующую силу.

Понятно, что работа равнодействующей силы равна изменению потенциальной энергии тела.

\[A = \Delta {W_п}\]

Введем ось \(y\), перпендикулярную поверхности Земли. Работу равнодействующей силы найдем по следующей формуле:

\[A = {F_y} \cdot \Delta y\]

Тогда:

\[{F_y} \cdot \Delta y = \Delta {W_п}\]

Поделим обе части равенства на \(\Delta t\), получим:

\[{F_y} \cdot \frac{{\Delta y}}{{\Delta t}} = \frac{{\Delta {W_п}}}{{\Delta t}}\]

Если промежуток времени \(\Delta t\) стремится к нулю (\(\Delta t \to 0\)), то отношение \(\frac{\Delta y}{\Delta t}\) равно проекции мгновенной скорости \(\upsilon_y\), a отношение \(\frac{\Delta W_п}{\Delta t}\) – это производная потенциальной энергии по времени, равная тангенсу угла наклона касательной к графику функции \({W_п}\left( t \right)\).

\[{F_y} \cdot {\upsilon _y} = \frac{{\Delta {W_п}}}{{\Delta t}}\]

Если равнодействующая сила минимальна, т.е. \(F_y=0\), тогда \(\frac{\Delta W_п}{\Delta t}=0\) – это условие выполняется для графика №1, в каждой точке которого производная равна нулю (тангенс угла наклона касательной также равен нулю).