На участке дороги, где для автотранспорта установлена предельная скорость 30 км/ч

Условие задачи:

На участке дороги, где для автотранспорта установлена предельная скорость 30 км/ч, водитель применил аварийное торможение. Определить скорость автомобиля перед торможением, если тормозной путь оказался 12 м. Коэффициент трения по сухому асфальту равен 0,6.

Задача №2.1.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon=30\) км/ч, \(S=12\) м, \(\mu=0,6\), \(\upsilon_0-?\)

Решение задачи:

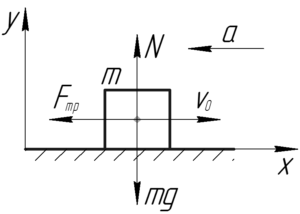Покажем на схеме все силы, действующие на автомобиль, и его начальную скорость \(\upsilon_0\). Применим законы Ньютона в проекции на оси \(x\) и \(y\).

\[\left\{ \begin{gathered}
ox:{F_{тр}} = ma \;\;\;\;(1)\hfill \\
oy:N – mg = 0 \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]

Сила трения \(F_{тр}\) равна произведению коэффициента трения \(\mu\) на силу нормальной реакции опоры \(N\), которая согласно выражению (2) равна силе тяжести \(mg\).

\[{F_{тр}} = \mu N = \mu mg\]

Подставим последнее выражение в формулу (1) и выразим ускорение тела:

\[\mu mg = ma \Rightarrow a = \mu g\]

Запишем формулу кинематики без времени, где \(\upsilon_1\) – конечная скорость автомобиля, равная нулю.

\[\upsilon _1^2 – \upsilon _0^2 =  – 2aS\]

\[\upsilon _0^2 = 2aS\]

\[\upsilon _0^2 = 2\mu gS \Rightarrow {\upsilon _0} = \sqrt {2\mu gS} \]

Давайте посчитаем какую же скорость имел автомобиль перед началом торможения.

\[{\upsilon _0} = \sqrt {2 \cdot 0,6 \cdot 10 \cdot 12}  = 12\; м/с = 43,2\; км/ч\]

Так как \({\upsilon _0} > \upsilon\), получается, водитель превысил скорость.

Ответ: 43,2 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.1.29 На тело, движущееся по горизонтальной поверхности, действуют следующие силы
2.1.31 Найти модуль изменения импульса шарика массой 20 г за 3 с свободного падения
2.1.32 Определить натяжение каната, к которому подвешена клеть подъемной машины