Решение: На вершине шара радиусом 30 см лежит небольшая шайба. После легкого толчка

Условие задачи:

На вершине шара радиусом 30 см лежит небольшая шайба. После легкого толчка шайба начинает соскальзывать. После спуска на какую высоту от вершины шара шайба оторвется от шара? Трением пренебречь.

Задача №2.8.40 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=30\) см, \(H_1-?\)

Решение задачи:

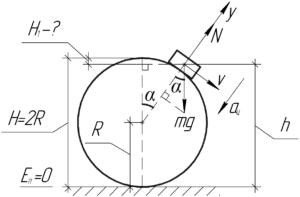Нарисуем произвольное положение шайбы на шаре. В этой точке нормаль к шару составляет угол \(\alpha\) с вертикалью (смотри рисунок). Запишем второй закон Ньютона в проекции на ось \(y\), которая совпадает с этой нормалью.

\[mg \cdot \cos \alpha – N = m{a_ц}\;\;\;\;(1)\]

Центростремительное ускорение шайбы можно определить по формуле:

\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\]

В этой формуле \(\upsilon\) – скорость шайбы, \(R\) – радиус кривизны траектории (радиус шара).

Тогда равенство (1) примет вид:

\[mg \cdot \cos \alpha – N = m\frac{{{\upsilon ^2}}}{R}\]

Если в этой точке шайба оторвется от поверхности шара, то сила реакции опоры \(N\) станет равна нулю:

\[N = 0\]

\[mg \cdot \cos \alpha = m\frac{{{\upsilon ^2}}}{R}\]

\[{\upsilon ^2} = gR \cdot \cos \alpha \;\;\;\;(2)\]

Теперь применим закон сохранения энергии. Нуль потенциальной энергии выберем на уровне стола. Тогда у шайбы в начальный момент времени имеется только потенциальная энергия, в точке отрыва от шара – и потенциальная, и кинетическая.

\[mgH = \frac{{m{\upsilon ^2}}}{2} + mgh\]

Очевидно, что начальная высота шайбы \(H\) равна двум радиусам шара, а конечная высота шайбы \(h\) – выражению \(R\left( {1 + \cos \alpha } \right)\) (смотри рисунок).

\[H = 2R\]

\[h = R\left( {1 + \cos \alpha } \right)\]

Тогда:

\[mg \cdot 2R = \frac{{m{\upsilon ^2}}}{2} + mg \cdot R\left( {1 + \cos \alpha } \right)\]

\[mgR\left( {1 – \cos \alpha } \right) = \frac{{m{\upsilon ^2}}}{2}\]

\[{\upsilon ^2} = 2gR\left( {1 – \cos \alpha } \right)\;\;\;\;(3)\]

Приравняем (2) и (3):

\[gR \cdot \cos \alpha = 2gR\left( {1 – \cos \alpha } \right)\]

\[\cos \alpha = 2 – 2\cos \alpha \]

\[\cos \alpha = \frac{2}{3}\]

Искомую высоту \(H_1\) можно найти таким образом:

\[{H_1} = H – h\]