Решение: Небольшое тело соскальзывает по наклонной плоскости, переходящей в мертвую

Условие задачи:

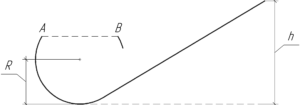Небольшое тело соскальзывает по наклонной плоскости, переходящей в мертвую петлю, в которой вырезана дуга, симметричная относительно вертикального диаметра. Радиус петли \(R=1\) м, хорда \(AB = R\sqrt 3\). Определить высоту, с которой должно опускаться тело, чтобы из точки А оно попало в точку B, двигаясь по воздуху. Трением и сопротивлением воздуха пренебречь.

Задача №2.8.49 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=1\) м, \(L = R\sqrt 3\), \(h-?\)

Решение задачи:

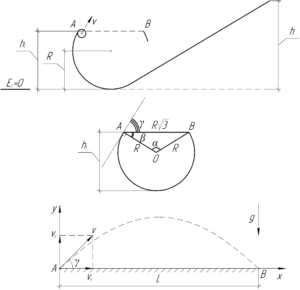Для начала разберем с геометрией. На средней части схемы изображена петля с вырезанной дугой. Чтобы найти центральный угол \(\alpha\) воспользуемся теоремой косинусов.

\[3{R^2} = {R^2} + {R^2} – 2R \cdot R \cdot \cos \alpha \]

\[3{R^2} = 2{R^2} – 2{R^2} \cdot \cos \alpha \]

\[3 = 2 – 2\cos \alpha \]

\[\cos \alpha = – \frac{1}{2}\]

Косинус угла \(\alpha\) отрицательный, поскольку этот угол тупой, что можно и видеть на рисунке.

\[\alpha = 120^\circ \]

Найдем угол \(\beta\) между хордой и радиусом. Рассматриваемый треугольник ABO равнобедренный, значит угол \(\beta\) можно найти из следующего соотношения, поскольку сумма всех углов треугольника равна 180°:

\[\beta = \frac{{180^\circ – \alpha }}{2}\]

\[\beta = \frac{{180^\circ – 120^\circ }}{2} = 30^\circ \]

Также необходимо найти угол \(\gamma\) между касательной (поскольку по ней будет направлена скорость тела) в точке A и хордой. Так как между касательной и радиусом угол прямой, то из рисунка видна, что угол \(\gamma\) равен:

\[\gamma = 90^\circ – \beta \]

\[\gamma = 90^\circ – 30^\circ = 60^\circ \]

Перейдем к физике. Так как потери энергии отсутствуют, то воспользуемся законом сохранения энергии. Нулевой уровень потенциальной энергии выберем на уровне поверхности стола. В начальный момент времени на наклонной плоскости тело имело потенциальную энергию \(mgh\), в точке A тело уже имеет потенциальную энергию \(mgh_1\) и кинетическую энергию \(\frac{{m{\upsilon ^2}}}{2}\).

\[mgh = \frac{{m{\upsilon ^2}}}{2} + mg{h_1}\;\;\;\;(1)\]

Высота тела \(h_1\) от стола в точке A, очевидно, равна (смотри схему):

\[{h_1} = R\left( {1 + \sin \beta } \right)\]

\[{h_1} = R\left( {1 + \sin 30^\circ } \right) = \frac{{3R}}{2}\;\;\;\;(2)\]

Теперь рассмотрим участок движения тела по воздуху. По сути это классическая задача на движение тела, брошенного под углом к горизонту. Думаю, все решающие эту задачу знают кинематику, поэтому оставлю объяснения и запишу формулу для дальности полета \(L\) (равная длине хорды AB):

\[L = \upsilon \cdot \cos \gamma \cdot 2t\]

Здесь \(t\) – время движения тела до верхней точки своей траектории, которую можно найти по такой формуле:

\[t = \frac{{\upsilon \cdot \sin \gamma }}{g}\]

Тогда:

\[L = \upsilon \cdot \cos \gamma \cdot 2\frac{{\upsilon \cdot \sin \gamma }}{g} = \frac{{{\upsilon ^2}\sin 2\gamma }}{g}\]

Так как по условию \(L = R\sqrt 3\) и \(\gamma = 60^\circ \), то:

\[R\sqrt 3 = \frac{{{\upsilon ^2}\sin 120^\circ }}{g}\]

\[{\upsilon ^2} = \frac{{gR\sqrt 3 }}{{\sin 120^\circ }}\]

\[{\upsilon ^2} = 2gR\;\;\;\;(3)\]

Подставим (2) и (3) в (1), получим:

\[mgh = mgR + mg\frac{{3R}}{2}\]

\[h = \frac{{5R}}{2}\]