Нить может выдержать силу натяжения 25,4 Н. На нити подвесили тело массой 2 кг

Условие задачи:

Нить может выдержать силу натяжения 25,4 Н. На нити подвесили тело массой 2 кг. На какой максимальный угол можно отклонить тело от положения равновесия, чтобы нить не разорвалась, когда тело будет проходить положение равновесия?

Задача №2.4.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(T=25,4\) Н, \(m=2\) кг, \(\alpha-?\)

Решение задачи:

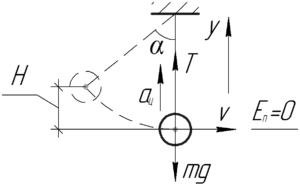В условии этой задачи уже сказано, что сила натяжения нити будет принимать своё максимальное значение, когда тело будет находиться в положении равновесия. Давайте запишем второй закон Ньютона для этого положения в проекции на ось \(y\) (смотрите схему):

\[T – mg = m{a_ц}\]

Пусть в положении равновесия скорость тела равна \(\upsilon\), а длина нити равна \(l\). В этом случае центростремительное ускорение \(a_ц\) можно найти по такой формуле:

\[{a_ц} = \frac{{{\upsilon ^2}}}{l}\]

Тогда:

\[T – mg = m\frac{{{\upsilon ^2}}}{l}\]

\[T = m\left( {g + \frac{{{\upsilon ^2}}}{l}} \right)\;\;\;\;(1)\]

Чтобы найти квадрат скорости, применим закон сохранения энергии для крайнего положения тела и для положения равновесия. Уровень нуля потенциальной энергии выберем на уровне положения равновесия тела.

\[mgH = \frac{{m{\upsilon ^2}}}{2}\]

Из схемы видно, что:

\[H = l – l \cdot \cos \alpha  = l\left( {1 – \cos \alpha } \right)\]

\[mgl\left( {1 – \cos \alpha } \right) = \frac{{m{\upsilon ^2}}}{2}\]

\[{\upsilon ^2} = 2gl\left( {1 – \cos \alpha } \right)\]

Полученное подставим в (1):

\[T = m\left( {g + \frac{{2gl\left( {1 – \cos \alpha } \right)}}{l}} \right)\]

\[T = mg\left( {3 – 2\cos \alpha } \right)\]

Осталось только выразить угол \(\alpha\):

\[\alpha  = \arccos \left( {\frac{3}{2} – \frac{T}{{2mg}}} \right)\]

Задача решена в общем виде. Теперь считаем ответ:

\[\alpha  = \arccos \left( {\frac{3}{2} – \frac{{25,4}}{{2 \cdot 2 \cdot 10}}} \right) = 30^\circ  = \frac{\pi }{6}\]

Ответ: \(\frac{\pi }{6}\).

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.22 На легкой нерастяжимой нити подвешен тяжелый шарик. На какой угол нужно отвести
2.4.24 По гладкому столу вращается груз, прикрепленный к центру вращения пружиной
2.4.25 Поезд движется по закруглению со скоростью 50 км/ч. Шарик, подвешенный в вагоне