Решение: Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г

Условие задачи:

Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г, начальная скорость дроби 320 м/с, а выстрел длится 0,05 с.

Задача №2.10.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=35\) г, \(\upsilon_0=320\) м/с, \(\Delta t = 0,05\) с, \(F-?\)

Решение задачи:

Силу отдачи можно определить из второго закона Ньютона, записанного в общем виде:

\[F = \frac{{\Delta p}}{{\Delta t}}\;\;\;\;(1)\]

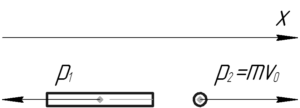
Поскольку иного не сказано в условии, то будем считать, что охотник держит ружье горизонтально. Система “ружье – дробь” замкнута вдоль горизонтальной оси \(x\), так как вдоль этой оси не действуют никакие внешние силы. В таком случае справедлив закон сохранения импульса в проекции на ось \(x\):

\[0 = – {p_1} + {p_2}\]

\[{p_1} = {p_2}\]

Здесь \(p_1\) – импульс, полученный ружьем при выстреле, \(p_2\) – импульс дроби, который равен \(m{\upsilon _0}\):

\[{p_1} = m{\upsilon _0}\]

Так как начальный импульс ружья, очевидно, равен нулю, то понятно, что изменение импульса ружья равно:

\[\Delta p = m{\upsilon _0}\;\;\;\;(2)\]

Подставим (2) в (1), тогда получим:

\[F = \frac{{m{\upsilon _0}}}{{\Delta t}}\]

Обязательно проверяем, все ли численные данные задачи даны в системе СИ – видно, что нужно перевести массу дроби.

\[35\; г = \frac{{35}}{{1000}}\; кг = 0,035\; кг\]

Теперь посчитаем ответ.

\[F = \frac{{0,035 \cdot 320}}{{0,05}} = 224\; Н\]