Определить силу, действующую на летчика, выводящего самолет из пикирования

Условие задачи:

Определить силу, действующую на летчика, выводящего самолет из пикирования. Скорость самолета 720 км/ч, радиус – 400 м, масса летчика – 75 кг.

Задача №2.4.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon=720\) км/ч, \(R=400\) м, \(m=75\) кг, \(N-?\)

Решение задачи:

В условии задачи имеется ввиду, что нужно найти силу реакции опоры \(N\).

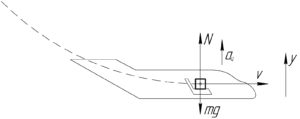
В тот момент, когда летчик выводит самолет из пикирования, на него действуют две силы: сила реакции опоры со стороны сиденья \(N\) и сила тяжести \(mg\). Причем если записать второй закон Ньютона в проекции на оси \(y\), то получим:

\[N – mg = m{a_ц}\]

Если нам известна скорость самолета \(\upsilon\) и радиус кривизны траектории \(R\), то найти центростремительное ускорение самолета можно по формуле:

\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\]

Тогда:

\[N – mg = m\frac{{{\upsilon ^2}}}{R}\]

\[N = m\left( {g + \frac{{{\upsilon ^2}}}{R}} \right)\]

Переведем скорость самолета в систему СИ:

\[720\; км/ч = \frac{{720 \cdot 1000}}{{1 \cdot 3600}}\; м/с = 200\; м/с\]

Только теперь можно считать ответ:

\[N = 75 \cdot \left( {10 + \frac{{{{200}^2}}}{{400}}} \right) = 8250\; Н = 8,25\; кН\]

Ответ: 8,25 кН.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.8 На горизонтальной вращающейся платформе на расстоянии 1,15 м от её вертикальной
2.4.10 Поезд движется по закруглению радиуса 765 м со скоростью 72 км/ч. Определить
2.4.11 Трактор массой 8 т проходит по мосту со скоростью 36 км/ч. Какова сила давления