Определить силу взаимодействия тела массой 2 кг и Земли, если тело удалено от

Условие задачи:

Определить силу взаимодействия тела массой 2 кг и Земли, если тело удалено от её поверхности на 4 земных радиуса.

Задача №2.5.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=2\) кг, \(h=4R\), \(F_т-?\)

Решение задачи:

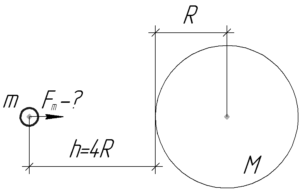Силу взаимодействия тела, находящегося на некоторой высоте, с Землей найдем из закона всемирного тяготения:

\[{F_т} = G\frac{{Mm}}{{{{\left( {R + h} \right)}^2}}}\]

Так как по условию \(h=4R\), то:

\[{F_т} = G\frac{{Mm}}{{{{\left( {R + 4R} \right)}^2}}} = G\frac{{Mm}}{{25{R^2}}}\]

Можно считать численный ответ по этой формуле, но это долго и многие совершают ошибки. Гораздо легче заметить, что:

\[g = G\frac{M}{{{R^2}}}\]

Поэтому:

\[{F_т} = \frac{{mg}}{{25}}\]

Посчитаем ответ:

\[{F_т} = \frac{{2 \cdot 10}}{{25}} = 0,8\; Н\]

Ответ: 0,8 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.5.1 Во сколько раз уменьшится сила тяготения тела к Земле при удалении его
2.5.3 Во сколько раз ускорение свободного падения около поверхности Земли больше
2.5.4 Искусственный спутник Земли движется на высоте 12800 км. Найти скорость движения