Решение: Определите время подъема камня массой 1 кг, брошенного под углом к горизонту

Условие задачи:

Определите время подъема камня массой 1 кг, брошенного под углом к горизонту, если начальный импульс камня, равный 10 кг·м/с, больше импульса в верхней точке траектории в два раза.

Задача №2.8.41 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=1\) кг, \(p_0=10\) кг·м/с, \(p_0=2p_1\), \(t-?\)

Решение задачи:

Согласно второму закону Ньютона, записанному в общем виде, равнодействующая сила равна отношению изменения импульса к интервалу времени действия силы:

\[F = \frac{{\Delta p}}{{\Delta t}}\]

На тело действует только сила тяжести, поэтому:

\[mg = \frac{{\Delta p}}{{\Delta t}}\;\;\;\;(1)\]

\[\Delta t = \frac{{\Delta p}}{{mg}}\]

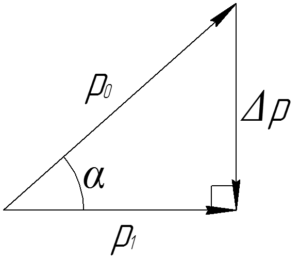
Нам необходимо найти изменение импульса, для этого нарисуем векторный треугольник (смотри схему). Если выражение (1) записать в векторной форме, то будет очевидно, что вектор изменения импульса должен быть направлен как и сила тяжести, то есть вертикально.

\[m\overrightarrow g = \frac{{\overrightarrow {\Delta p} }}{{\Delta t}}\;\;\;\;(2)\]

Вектор \(\overrightarrow {{p_1}}\) направлен горизонтально, так как в наивысшей точке траектории скорость направлена горизонтально. Получается, что наш векторный треугольник – прямоугольный. Тогда:

\[\cos \alpha = \frac{{{p_1}}}{{{p_0}}}\]

Так как по заданию \(p_0=2p_1\), то:

\[\cos \alpha = \frac{{{p_1}}}{{2{p_1}}} = \frac{1}{2}\]

\[\alpha = {60^0}\]

Значит:

\[\sin \alpha = \frac{{\Delta p}}{{{p_1}}}\]

\[\Delta p = {p_1}\sin \alpha \]

Последнее выражение подставим в (2) и получим решение задачи.

\[\Delta t = \frac{{{p_1}\sin \alpha }}{{mg}}\]

Посчитаем ответ:

\[\Delta t = \frac{{10 \cdot \sin 60^\circ }}{{1 \cdot 10}} = 0,866\; с = 866\; мс\]