Условие задачи:
По абсолютно гладкой поверхности движется со скоростью 6 м/с ящик с песком массой 9 кг. В песок попадает гиря массой 1 кг, отпущенная без начальной скорости с десятиметровой высоты. Определить скорость ящика после попадания в него гири.
Задача №2.10.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=6\) м/с, \(M=9\) кг, \(m=1\) кг, \(h=10\) м, \(\upsilon-?\)
Решение задачи:
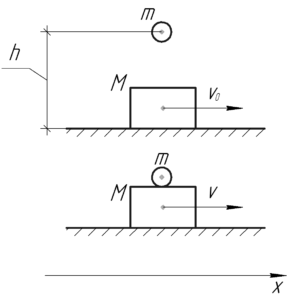 На систему «ящик — гиря» вдоль оси \(x\) не действуют никакие силы, то есть система замкнута вдоль этой оси. Значит, мы можем записать закон сохранения импульса в проекции на эту ось:
На систему «ящик — гиря» вдоль оси \(x\) не действуют никакие силы, то есть система замкнута вдоль этой оси. Значит, мы можем записать закон сохранения импульса в проекции на эту ось:
\[M{\upsilon _0} = \left( {m + M} \right)\upsilon \]
В этом уравнении одно неизвестное — искомая скорость \(\upsilon\). Выразим её и получим решение задачи в общем виде:
\[\upsilon = \frac{{M{\upsilon _0}}}{{m + M}}\]
Подставим в эту формулу исходные численные данные и посчитаем ответ:
\[\upsilon = \frac{{9 \cdot 6}}{{1 + 9}} = 5,4\; м/с = 19,4\; км/ч\]
Интересно, что совсем неважно, с какой высоты падает гиря. Она (высота) имела бы значение только при расчете выделившейся при абсолютно неупругом ударе теплоты.
Ответ: 19,4 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.9.7 На горизонтальной поверхности в 3 м от вертикальной стенки находится шар массой
2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.3 Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе

 icodepro.ru
icodepro.ru
а то что гиря падает с 10метровой высоты не имеет значения? Она будет иметь свой импульс m(gt)
Это не имеет значения, поскольку импульс гири направлен по оси \(y\)