Условие задачи:
По наклонной плоскости с углом наклона 30° к горизонту скользит вниз тело. Определить скорость тела в конце второй секунды скольжения, если коэффициент трения 0,15.
Задача №2.3.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=30^\circ\), \(\mu=0,15\), \(t=2\) с, \(\upsilon-?\)
Решение задачи:
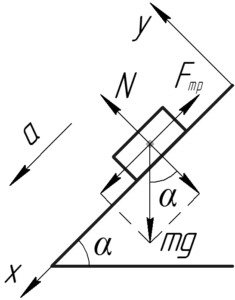 Если тело движется равноускоренно из состояния покоя, то его скорость через время \(t\) можно узнать по формуле:
Если тело движется равноускоренно из состояния покоя, то его скорость через время \(t\) можно узнать по формуле:
\[\upsilon = at\;\;\;\;(1)\]
Получается, что нам нужно определить ускорение тела \(a\). Чтобы это сделать, покажем на схеме все силы, действующие на тело, и запишем второй закон Ньютона в проекции на ось \(x\):
\[ma = mg \cdot \sin \alpha – {F_{тр}}\;\;\;\;(2)\]
Тело покоится вдоль оси \(y\), применим первый закон Ньютона в проекции на ось \(y\):
\[N = mg \cdot \cos \alpha \;\;\;\;(3)\]
Запишем формулу для определения силы трения скольжения:
\[{F_{тр}} = \mu N\]
Сила реакции опоры \(N\) определяется формулой (3), поэтому:
\[{F_{тр}} = \mu mg \cdot \cos \alpha \;\;\;\;(4)\]
Подставим (4) в (2), тогда:
\[ma = mg \cdot \sin \alpha – \mu mg \cdot \cos \alpha \]
\[a = g\left( {\sin \alpha – \mu \cos \alpha } \right)\]
Полученное выражения для ускорения подставим в формулу (1), в итоге получим решение задачи в общем виде:
\[\upsilon = gt\left( {\sin \alpha – \mu \cos \alpha } \right)\]
Посчитаем численный ответ:
\[\upsilon = 10 \cdot 2 \cdot \left( {\sin 30^\circ – 0,15 \cdot \cos 30^\circ } \right) = 7,4\; м/с = 26,65\; км/ч\]
Ответ: 26,65 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.3.3 По канатной дороге, идущей с уклоном 30 градусов к горизонту, опускается вагонетка
2.3.5 Санки можно удержать на ледяной горке с уклоном 0,2 (отношение высоты к длине)
2.3.6 Тело массой 1 кг, имеющее у основания наклонной плоскости скорость 6 м/с

 icodepro.ru
icodepro.ru
Добрый день, такой задачи вроде не было, буду благодарен за помощь!
Через какое время тело, скользящее вверх по шероховатой прямолинейной поверхности, наклоненной к горизонту под углом ?=35?, начнет опускаться.
Начальная скорость тела равна 7 м/с, ускорение свободного падения g считать равным 9,81 м/с2. Коэффициент трения скольжения f=0,4
Помогите пожалуйста!с каким значением коэфициента трения человек может поднятся в гору длиной 10 метров,углом наклона поверхности 0,1 rad за 10 секунд,(двигаясь с одинаковой скоростью,без начальной скорости)?
Помогите По наклонной плоскости с углом наклона ? = 300 съезжает лыжник массой m1 = 70 кг. Проехав расстояние l=20 м от вершины, он стреляет вверх сигнальной ракетой. Масса ракеты m2 = 0,5 кг, ее начальная скорость v2 = 85 м/с. Трение не учитывать. Определить скорость v1 лыжника после выстрела. (14,4 м/с)
По наклонной плоскости (угол наклона 300) равномерно тянут за канат груз массой 40 кг. Коэффициент трения 0,2. Груз поднимается на высоту10 м за 2 с. Определите силу натяжения каната.
Пмогите,пожалуйста??
Здравствуйте,помогите пожалуйста,буду очень признательна
Вот задача:По наклонной плоскости (угол наклона 300) равномерно тянут за канат груз массой 40 кг. Коэффициент трения 0,2. Груз поднимается на высоту 10 м за 2 с. Определите силу натяжения каната.
Можете пожалуйста помочь.
Тело, масса которого m=1 кг, движется вниз по наклонной плоскости с углом наклона угол =30 градусов под действием силы F=2 Н, направленной горизонтально. Определить ускорение тела а, если коэффициент трения тела о плоскость 0,2.
Бездоказательно приму, что сила \(F\) направлена как на рисунке. Вообще говоря, возможны такие исходные данные, при которых тело будет скользить вниз и при противоположном направлении силы \(F\). Решая задачу, я конечно проверил данное предположение (сила действительно направлена как показано на рисунке), но с Вашего позволения доказательство я здесь приводить не буду.
Запишем второй закон Ньютона в проекциях на оси координат:\[\left\{ \begin{gathered}
F\cos \alpha + mg\sin \alpha – {F_{тр}} = ma \hfill \\
N + F\sin \alpha – mg\cos \alpha = 0 \hfill \\
\end{gathered} \right.\]Сила нормальной реакции опоры \(N\) равна:\[N = mg\cos \alpha – F\sin \alpha \]Тогда сила трения скольжения \(F_{тр}\) равна:\[{F_{тр}} = \mu N = \mu mg\cos \alpha – \mu F\sin \alpha \]В таком случае первое уравнение примет вид:\[F\cos \alpha + mg\sin \alpha – \mu mg\cos \alpha + \mu F\sin \alpha = ma\]\[F\left( {\cos \alpha + \mu \sin \alpha } \right) + mg\left( {\sin \alpha – \mu \cos \alpha } \right) = ma\]В итоге ускорение равно:\[a = \frac{{F\left( {\cos \alpha + \mu \sin \alpha } \right) + mg\left( {\sin \alpha – \mu \cos \alpha } \right)}}{m}\]Численный ответ равен:\[a = \frac{{2 \cdot \left( {\cos 30^\circ + 0,2 \cdot \sin 30^\circ } \right) + 1 \cdot 9,81 \cdot \left( {\sin 30^\circ – 0,2 \cdot \cos 30^\circ } \right)}}{1} = 5,14\;м/с^2\]
Помогите пожалуйста Тело скользит вверх по гладкой прямолинейной поверхности, наклоненной к горизонту под углом ? = 60°. Начальная скорость тела равна v0 = 44 м/с, ускорение свободного падения g = 9,8 м/с2. Тело начнет опускаться в момент времени t, равный
В Вашем случае тело будет двигаться по наклонной плоскости равнозамедленно с ускорением, равным (так как плоскость гладкая, и на тело вдоль наклонной плоскости действует только проекция силы тяжести):\[a = g\sin \alpha \]Скорость при равнозамедленном движении определяют по формуле:\[\upsilon = {\upsilon _0} – at\]В верхней точке тело на мгновение остановится \(\upsilon = 0\), затем оно начнет движение обратно вниз, поэтому:\[0 = {\upsilon _0} – at\]Откуда искомое время равно:\[t = \frac{{{\upsilon _0}}}{a}\]Учитывая все вышесказанное, имеем:\[t = \frac{{{\upsilon _0}}}{{g\sin \alpha }}\]Численный ответ равен:\[t = \frac{{44}}{{9,8 \cdot \sin 60^\circ }} = 5,2\;с\]
Помогите, пожалуйста
По наклонной плоскости с углом наклона к горизонту, равным 60 градусов, скользит тело. Определите скорость тела в конце пятой секунды от начала скольжения, если коэффициент трения равен 0,3. Начальная скорость равна 0,5 м/с
Решение абсолютно такое же, численный ответ в Вашем случае равен:\[\upsilon = 9,81 \cdot 5 \cdot \left( {\sin 60^\circ – 0,3 \cdot \cos 60^\circ } \right) = 42,4\;м/с\]
Работа трения (g = 10 м/с^2) при скольжении тела массой 4 кг вверх от основания наклонной плоскости со скоростью 7 м/с поднимается на высоту 0,5 м
Работа силы трения будет равна разности конечной потенциальной энергии и начальной кинетической:\[A = mgh – \frac{{m{\upsilon ^2}}}{2}\]\[A = 4 \cdot 10 \cdot 0,5 – \frac{{4 \cdot {7^2}}}{2} = – 78\;Дж\]Работа силы трения отрицательна, так как сила направлена противоположно перемещению.
помогите, пожалуйста
две наклонные плоскости имеют одинаковое основание. Каков коэффициент трения, если время соскальзывания с плоскости с угла наклона a = 45 градусов равно времени соскальзывания этого же тела с плоскости с углом наклона b= 60 градусов?
Определим время соскальзывания тела с наклонной плоскости с основанием \(L\) и углом при основании \(\alpha\), используя найденное при решении вышеприведенной задачи ускорение \(a\):\[\left\{ \begin{gathered}
S = \frac{L}{{\cos \alpha }} \hfill \\
S = \frac{{a{t^2}}}{2} = \frac{{g\left( {\sin \alpha – \mu \cos \alpha } \right){t^2}}}{2} \hfill \\
\end{gathered} \right.\]Тогда:\[\frac{L}{{\cos \alpha }} = \frac{{g\left( {\sin \alpha – \mu \cos \alpha } \right){t^2}}}{2}\]Откуда получим:\[{t^2} = \frac{{2L}}{{g\cos \alpha \left( {\sin \alpha – \mu \cos \alpha } \right)}}\]\[t = \sqrt {\frac{{2L}}{{g\cos \alpha \left( {\sin \alpha – \mu \cos \alpha } \right)}}} \]Время соскальзывания будет одинаковым у двух наклонных плоскостей с углом при основании \(\alpha_1\) и \(\alpha_2\), если:\[\cos {\alpha _1}\left( {\sin {\alpha _1} – \mu \cos {\alpha _1}} \right) = \cos {\alpha _2}\left( {\sin {\alpha _2} – \mu \cos {\alpha _2}} \right)\]Раскроем скобки:\[\cos {\alpha _1}\sin {\alpha _1} – \mu {\cos ^2}{\alpha _1} = \cos {\alpha _2}\sin {\alpha _2} – \mu {\cos ^2}{\alpha _2}\]\[\cos {\alpha _1}\sin {\alpha _1} – \cos {\alpha _2}\sin {\alpha _2} = \mu {\cos ^2}{\alpha _1} – \mu {\cos ^2}{\alpha _2}\]\[\cos {\alpha _1}\sin {\alpha _1} – \cos {\alpha _2}\sin {\alpha _2} = \mu \left( {{{\cos }^2}{\alpha _1} – {{\cos }^2}{\alpha _2}} \right)\]\[\mu = \frac{{\cos {\alpha _1}\sin {\alpha _1} – \cos {\alpha _2}\sin {\alpha _2}}}{{{{\cos }^2}{\alpha _1} – {{\cos }^2}{\alpha _2}}}\]Численный ответ равен:\[\mu = \frac{{\cos 45^\circ \cdot \sin 45^\circ – \cos 60^\circ \cdot \sin 60^\circ }}{{{{\cos }^2}45^\circ – {{\cos }^2}60^\circ }} = 0,27\]
помогите с такой вот задачкой буду очень благодарен
Мяч массой m = 1 кг катится по горизонтальной плоскости с установкой.
скоростью ? = 2 м/с. Найти кинетическую энергию шара. Какой путь пройдет пуля
вверх по поверхности, угол наклона которой ? = 30 градусов к горизонту?
Так мяч, шар или пуля, не могу понять?
сори переводчик с украинского так перевел не посмотрел но уже с задачей справился спасибо)

Можете пожалуйста помочь, с этой задачей?
Могу, если мне предоставят её нормальное условие
Здравствуйте! а как найти коэффициент трения, если тело скользит вниз по наклонной плоскости 30 градусов к горизонту, и к концу 5-й секунды проедет расстояние 10 метров?
Пройденный путь определяется по формуле:\[S = \frac{{a{t^2}}}{2}\]Учитывая выражения для нахождения ускорения (см. решение выше), имеем:\[S = \frac{{g\left( {\sin \alpha – \mu \cos \alpha } \right){t^2}}}{2}\]Из этой формулы нужно выразить коэффициент трения:\[\sin \alpha – \mu \cos \alpha = \frac{{2S}}{{g{t^2}}}\]\[\mu \cos \alpha = \sin \alpha – \frac{{2S}}{{g{t^2}}}\]\[\mu = {\text{tg}}\alpha – \frac{{2S}}{{g{t^2}\cos \alpha }}\]Численный ответ равен:\[\mu = {\text{tg}}30^\circ – \frac{{2 \cdot 10}}{{10 \cdot {5^2} \cdot \cos 30^\circ }} = 0,48\]
Добрый день! Объясните, пожалуйста, почему при подсчете численного ответа вы принимаете g=10? Это постоянная сила земного притяжения?
Это округленное значение ускорения свободного падения \(g\) (такое значение принимают на ЕГЭ)
Помогите пожалуйста.

Рисунок
Масса тела №2 = 4кг
Тело №2 = Какую максимальную массу может иметь тело,
чтобы система оставалась неподвижной? Коэффициент трения 0,1.
У Вас опечатка, в Вашей задаче нужно найти массу тела 1.
На тело 1 действуют 2 силы (сила тяжести и сила натяжения нити), записав первый закон Ньютона в проекции на вертикальную ось, мы получим:\[T = {m_1}g\;\;\;\;(1)\]
На тело 2 действуют уже 4 силы (сила тяжести, сила натяжения нити, сила трения покоя и сила нормальной реакции опоры), запишем первый закон Ньютона в проекции на ось, перпендикулярную наклонной плоскости, и на ось, параллельную наклонной плоскости:\[\left\{ \begin{gathered}
N = {m_2}g\cos \alpha\;\;\;\;(2) \hfill \\
{F_{тр}} + {m_2}g\sin \alpha = T\;\;\;\;(3) \hfill \\
\end{gathered} \right.\]Условие, при котором система будет оставаться неподвижной:\[{F_{тр}} \leq \mu N\;\;\;\;(4)\]В (3) подставим (1):\[{F_{тр}} + {m_2}g\sin \alpha = {m_1}g\]\[{F_{тр}} = {m_1}g – {m_2}g\sin \alpha \]\[{F_{тр}} = \left( {{m_1} – {m_2}\sin \alpha } \right)g\;\;\;\;(5)\]В (4) подставим (5) и (2):\[\left( {{m_1} – {m_2}\sin \alpha } \right)g \leq \mu {m_2}g\cos \alpha \]\[{m_1} – {m_2}\sin \alpha \leq \mu {m_2}\cos \alpha \]\[{m_1} \leq {m_2}\sin \alpha + \mu {m_2}\cos \alpha \]\[{m_1} \leq {m_2}\left( {\sin \alpha + \mu \cos \alpha } \right)\]Максимальная масса тела 1 равна:\[{m_1} = {m_2}\left( {\sin \alpha + \mu \cos \alpha } \right)\]Численный ответ:\[{m_1} = 4 \cdot \left( {\sin 30^\circ + 0,1 \cdot \cos 30^\circ } \right) = 2,35\;кг\]
Помогите пожалуйста

Полая сфера в первом случае соскальзывает без качения, а во втором – скатывается без
скольжение с вершины наклонной плоскости с углом наклона к горизонту 30? и длиной основания
4 м. Определить скорость сферы в конце спуска в обоих случаях
Скорость поступательного движения полой сферы в конце спуска в обоих случаях будем определять из следующей формулы:\[{\upsilon ^2} = 2aS\]\[\upsilon = \sqrt {2aS} \]Нам остается только найти ускорения в обоих случаях, рассмотрим каждый из них.
1) Первый случай (скольжение без качения). Направим ось \(x\) вдоль поверхности, далее запишем уравнение второго закона Ньютона в проекции на ось \(x\):\[ma = mg\sin \alpha \]\[a = g\sin \alpha \]Учитывая ранее полученную формулу, имеем:\[\upsilon = \sqrt {2g\sin \alpha S} \]Численный ответ равен:\[\upsilon = \sqrt {2 \cdot 10 \cdot \sin 30^\circ \cdot 4} = 6,3\;м/с\]
2) Второй случай (качение без скольжения). Запишем уравнение вращательного движения относительно точки касания сферы с поверхностью, использую теорему Штейнера:\[\left( {{I_0} + m{r^2}} \right)\frac{a}{r} = mgr\sin \alpha \]Момент инерции полой сферы \(I_0\) равен:\[{I_0} = \frac{2}{3}m{r^2}\]Тогда:\[\left( {\frac{2}{3}m{r^2} + m{r^2}} \right)\frac{a}{r} = mgr\sin \alpha \]\[\frac{5}{3}mra = mgr\sin \alpha \]\[a = \frac{3}{5}g\sin \alpha \]Учитывая ранее полученную формулу, имеем:\[\upsilon = \sqrt {\frac{6}{5}g\sin \alpha S} \]Численный ответ равен:\[\upsilon = \sqrt {\frac{6}{5} \cdot 10 \cdot \sin 30^\circ \cdot 4} = 4,9\;м/с\]
Добрый день, буду благодарен если поможете!
Одно тело начинает соскальзывать с поверхности длиной 2 м, наклоненной под
углом 30° к горизонту, с начальной скоростью 5 м/с, а другое тело с такой
самой начальной скоростью начинает двигаться вверх. Трением пренибречь. Найти время подьема и соскальзования.
Еще раз, спасибо.
1) Скольжение вниз. Ускорение по модулю равно (из 2-го закона Ньютона в проекции на ось \(x\), которая направлена вниз вдоль наклонной поверхности):\[a = g\sin \alpha \]Запишем уравнение движения (в данном случае оно равноускоренное):\[S = {\upsilon _0}t + \frac{{a{t^2}}}{2}\]Чтобы найти время \(t\), решим это квадратное уравнение относительно \(t\):\[\frac{{a{t^2}}}{2} + {\upsilon _0}t – S = 0\]\[D = \upsilon _0^2 + 4\frac{a}{2}S = \upsilon _0^2 + 2aS\]\[t = \frac{{ – {\upsilon _0} \pm \sqrt {\upsilon _0^2 + 2aS} }}{a}\]Отрицательный корень нам не интересен, поэтому:\[t = \frac{{ – {\upsilon _0} + \sqrt {\upsilon _0^2 + 2aS} }}{a}\]Учитывая выражение для ускорения \(a\), имеем:\[t = \frac{{ – {\upsilon _0} + \sqrt {\upsilon _0^2 + 2g\sin \alpha S} }}{{g\sin \alpha }}\]Численный ответ равен:\[t = \frac{{ – 5 + \sqrt {{5^2} + 2 \cdot 10 \cdot \sin 30^\circ \cdot 2} }}{{10 \cdot \sin 30^\circ }} = 0,34\;с\]
1) Скольжение вверх. Ускорение по модулю равно (из 2-го закона Ньютона в проекции на ось \(x\), которая направлена вверх вдоль наклонной поверхности):\[a = g\sin \alpha \]Запишем уравнение движения (в данном случае оно равнозамедленное):\[S = {\upsilon _0}t – \frac{{a{t^2}}}{2}\]Чтобы найти время \(t\), решим это квадратное уравнение относительно \(t\):\[\frac{{a{t^2}}}{2} – {\upsilon _0}t + S = 0\]\[D = \upsilon _0^2 – 4\frac{a}{2}S = \upsilon _0^2 – 2aS\]\[t = \frac{{{\upsilon _0} \pm \sqrt {\upsilon _0^2 – 2aS} }}{a}\]Нам интересно минимальное время, за которое тело доберется до вершины наклонной поверхности, поэтому:\[t = \frac{{{\upsilon _0} – \sqrt {\upsilon _0^2 – 2aS} }}{a}\]Учитывая выражение для ускорения \(a\), имеем:\[t = \frac{{{\upsilon _0} – \sqrt {\upsilon _0^2 – 2g\sin \alpha S} }}{{g\sin \alpha }}\]Численный ответ равен:\[t = \frac{{5 – \sqrt {{5^2} – 2 \cdot 10 \cdot \sin 30^\circ \cdot 2} }}{{10 \cdot \sin 30^\circ }} = 0,55\;с\]
помогите пожалуйста.
Тело скользит по наклонной плоскости, угол наклона которой к горизонту ? =30°: 1) определите ускорение тела, если коэффициент трения между телом и поверхностью плоскости k= 0,1; 2) найдите уголнаклона ?0, при котором тело не будет скользить по наклонной плоскости.
1) Ускорение определяется так же, как и в решении выше:\[a = g\left( {\sin \alpha – \mu \cos \alpha } \right)\]\[a = 10 \cdot \left( {\sin 30^\circ – 0,1 \cdot \cos 30^\circ } \right) = 4,13\;м/с^2\]
2) Тело не будет скользить, если:\[mg\sin \alpha \leq {F_{макс.тр.п}}\]\[mg\sin \alpha \leq \mu N\]\[mg\sin \alpha \leq \mu mg\cos \alpha \]\[\sin \alpha \leq \mu \cos \alpha \]\[tg\alpha \leq \mu \]\[\alpha \leq{\text{arctg}}\left( \mu \right)\]\[\alpha \leq {\text{arctg}}\left( {0,1} \right)\]\[\alpha \leq 5,71^\circ \]
Добрый день! подскажите, пожалуйста, а как определить скорость при ваших условиях задачи, но на расстоянии 10 метров?
\[{\upsilon ^2} = 2aS\]\[\upsilon = \sqrt {2aS} \]\[\upsilon = \sqrt {2g\left( {\sin \alpha – \mu \cos \alpha } \right)S} \]Численный ответ такой:\[\upsilon = \sqrt {2 \cdot 10 \cdot \left( {\sin 30^\circ – 0,15 \cdot \cos 30^\circ } \right) \cdot 10} = 8,6\;м/с\]
Не понимаю, как у вас получилось 2,72? у меня почему-то вычисляется 8,6
Прошу прощения за ошибку, ответ действительно 8,6 м/с
По наклонной плоскости с углом наклона к горизонту 300 скользит тело. Найти скорость тела в конце третьей секунды от начала скольжения, если коэффициент трения равен 0,25. Какое расстояние прошло тело за три секунды
Скорость определяете по формуле, которая получена выше:\[\upsilon = gt\left( {\sin \alpha – \mu \cos \alpha } \right)\]Путь можно найти по следующей формуле:\[S = \frac{{\left( {{\upsilon _0} + \upsilon } \right)t}}{2}\]Так как начальная скорость похоже равна нулю, то:\[S = \frac{{\upsilon t}}{2}\]Учитывая первую формулу, имеем:\[S = \frac{{g{t^2}\left( {\sin \alpha – \mu \cos \alpha } \right)}}{2}\]Численные ответы такие (угол \(\alpha=60^\circ\) у Вас):\[\upsilon = 10 \cdot 3 \cdot \left( {\sin 60^\circ – 0,25 \cdot \cos 60^\circ } \right) = 22,2\;м/с\]\[S = \frac{{10 \cdot {3^2} \cdot \left( {\sin 60^\circ – 0,25 \cdot \cos 60^\circ } \right)}}{2} = 33,3\;м\]
Здравствуйте, помогите решить, пожалуйста, буду очень признателен. Нигде найти не могу
Однородный цилиндр катится без скольжения по поверхности, наклоненной под углом 30 градусов к горизонту. Определить скорость цилиндра, когда он пройдет путь длиной 2 м. Через время цилиндр пройдет этот путь? Трением пренебречь.
Направим ось \(x\) вдоль поверхности, далее запишем уравнение второго закона Ньютона в проекции на ось \(x\) и основное уравнение вращательного движения цилиндра относительно его центра масс:\[\left\{ \begin{gathered}
ma = mg\sin \alpha – {F_{тр}} \hfill \\
I\varepsilon = M \hfill \\
\end{gathered} \right.\]Для сплошного диска момент инерции равен \(I = \frac{{m{r^2}}}{2}\), а угловое ускорение \(\varepsilon = \frac{a}{r}\). Понятно, что цилиндр вращается из-за силы трения \(F_{тр}\), плечо которой относительно оси вращения равно \(r\). Тогда:\[\left\{ \begin{gathered}
ma = mg\sin \alpha – {F_{тр}} \hfill \\
\frac{{m{r^2}}}{2} \cdot \frac{a}{r} = {F_{тр}} \cdot r \hfill \\
\end{gathered} \right.\]В итоге:\[a = \frac{2}{3}g\sin \alpha \]Скорость определим следующим образом:\[{\upsilon ^2} = 2aS\]\[\upsilon = \sqrt {2aS} \]\[\upsilon = \sqrt {\frac{4}{3}gS\sin \alpha } \]Время определим по формуле:\[t = \frac{\upsilon }{a}\]\[t = \sqrt {\frac{{3S}}{{g\sin \alpha }}} \]Численные ответы такие:\[\upsilon = \sqrt {\frac{4}{3} \cdot 9,8 \cdot 2 \cdot \sin 30^\circ } = 3,6\;м/с\]\[t = \sqrt {\frac{{3 \cdot 2}}{{9,8 \cdot \sin 30^\circ }}} = 1,1\;м\]
офигеть, неужели такое возможно))) класс)))
вауу, у вас такой крутой сайт, да ещё много пользователей, для которых вы так стараетесь и отвечаете на вопросы… ?
вам бы уже приложение создать… было бы классно и удобно и офлайн. и ещё там раздел отдельно с формулами… эх (просто мечтаю вслух)?
как вам предложение, м?
Спасибо за комплимент, очень приятно


Да, идея интересная, спасибо за предложение
У меня самого очень много идей, и я скорее испытываю недостаток времени, чем идей, надеюсь в будущем воплотим Ваше желание
pomogite pls) Найти ускорение куба если масса клина М, масса куба – m. угол
клина ?. Трение отсутствует.
Очень интересная задача! В ней клин, приставленный к стенке и движущийся вниз, толкает куб, находящийся на столе и из-за клина движущийся вправо. Решается достаточно просто, необходимо записать второй закон Ньютона для каждого из тел в направлении движения каждого тела:\[\left\{ \begin{gathered}
Mg – N\sin \alpha = M{a_1} \hfill \\
N\cos \alpha = m{a_2} \hfill \\
\end{gathered} \right.\]Нетрудно заметить, что ускорения (а также скорости и перемещения) связаны такой зависимостью:\[{a_2} = {a_1}tg\alpha \]Решая совместно три уравнения, Вы получите такой ответ (математику расписывать не буду, все достаточно просто, выражаете из второго уравнения системы \(N\), из связи ускорений – \(a_1\), и подставляете их в первое уравнение):\[{a_2} = \frac{{Mg \cdot tg\alpha }}{{M + m \cdot t{g^2}\alpha }}\]
Можете помочь?
Тело массой 2 кг соскальзывает с высоты 4 м вдоль наклонной плоскости, составляющей угол
45° с горизонтом, без начальной скорости. Найти скорость тела в конце наклонной плоскости,
если коэффициент трения скольжения равен 0,2?
Запишем закон сохранения энергии:\[mgH = \frac{{m{\upsilon ^2}}}{2} + {F_{тр}}L\]Силу трения скольжения в данном случае следует определять так:\[{F_{тр}} = \mu mg\cos \alpha \]Длину наклонной плоскости легко определить из прямоугольного треугольника:\[L = \frac{H}{{\sin \alpha }}\]Тогда:\[mgH = \frac{{m{\upsilon ^2}}}{2} + \mu mg\cos \alpha \frac{H}{{\sin \alpha }}\]\[gH = \frac{{{\upsilon ^2}}}{2} + \mu gH ctg \alpha \]\[{\upsilon ^2} = 2gH\left( {1 – \mu ctg \alpha } \right)\]\[\upsilon = \sqrt {2gH\left( {1 – \mu ctg \alpha } \right)} \]Численный ответ равен:\[\upsilon = \sqrt {2 \cdot 10 \cdot 4\left( {1 – 0,2 \cdot ctg 45^\circ } \right)} = 8\;м/с\]
Определить коэффициент скольжения при подрезании пласта почвы лезвием лемеха корпуса с культурной поверхностью отвала при угле трения 30 градусов
Скорее всего это задача из специализированного инженерного курса, а не по курсу общей физики, ничем помочь не могу
Здравствуйте, помогите пожалуйста с решением, никак не могу разобраться
Нужно узнать начальную скорость тела движущегося вверх по наклонной области.
Длина наклонной = 20м, угол наклона = 30 градусов, вес тела = 5кг, коэффициент трения = 0,1
Ваше условие неполное. Если решать из предположения, что тело остановится, достигнув края наклонной плоскости, то решение должно быть следующим. Запишем закон сохранения:\[\frac{{m{\upsilon ^2}}}{2} = mgh + {F_{тр}}L\]Так как сила трения равна \({F_{тр}} = \mu mg\cos \alpha \), высота наклонной плоскости равна \(h = L\sin \alpha \), то имеем:\[\frac{{m{\upsilon ^2}}}{2} = mgL\sin \alpha + \mu mgL\cos \alpha \]\[{\upsilon ^2} = 2\left( {gL\sin \alpha + \mu gL\cos \alpha } \right)\]\[{\upsilon ^2} = 2gL\left( {\sin \alpha + \mu \cos \alpha } \right)\]\[\upsilon = \sqrt {2gL\left( {\sin \alpha + \mu \cos \alpha } \right)} \]Численный ответ равен:\[\upsilon = \sqrt {2 \cdot 9,81 \cdot 20 \cdot \left( {\sin 30^\circ + 0,1 \cdot \cos 30^\circ } \right)} = 15,17\;м/с\]
Здравствуйте помогите решить!
Тело скользит по наклонной плоскости, которая образует угол 30 градусов с горизонтом. Коэффициент трения 0,2. ускорение тела?
Решается Ваша задача абсолютна также, как и та, что и приведена выше. То есть решение Вашей задачи в общем виде такое: \[a = g\left( {\sin \alpha – \mu \cos \alpha } \right)\] \[a = 10 \cdot \left( {\sin 30^{\circ} – 0,3 \cdot \cos 30^{\circ} } \right) = 2,4\;м/с^2\]
Объясните ,пожалуйста.Чтобы вытащить груз вверх по наклонной плоскости с углом 15 градусов ,нужно приложить силу 120 Н,а чтобы стянуть вниз,нужно приложить силу 15 Н. Найти коефициент трения,если в обоих случаях силы направлены вдоль наклонной плоскости.
Силу \(F_1\), которую нужно приложить, чтобы груз тащить (равномерно) вверх, можно найти так (первый закон Ньютона):\[{F_1} = mg\sin \alpha + \mu mg\cos \alpha \]Силу \(F_2\), которую нужно приложить, чтобы груз стянуть (равномерно) вниз, можно найти так (опять первый закон Ньютона):\[{F_2} = \mu mg\cos \alpha – mg\sin \alpha \]Оба эти уравнения складываете и вычитаете, тогда получите такую систему уравнений:\[\left\{ \begin{gathered}
{F_1} + {F_2} = 2\mu mg\cos \alpha \hfill \\
{F_1} – {F_2} = 2mg\sin \alpha \hfill \\
\end{gathered} \right.\]
Делим верхнее уравнение на нижнее:\[\frac{{{F_1} + {F_2}}}{{{F_1} – {F_2}}} = \frac{\mu }{{tg\alpha }}\]Окончательно получим:\[\mu = \frac{{{F_1} + {F_2}}}{{{F_1} – {F_2}}}tg\alpha \]
\[\mu = \frac{{120 + 15}}{{120 – 15}} \cdot tg15^\circ = 0,345\]
А если ничего не дано. Вот условие: На наклонной плоскости находится тело массой m. Чему равны сила упругости плоскости и угол наклона плоскости к горизонту, если в горизонтальном направлении к телу приложена внешняя сила F, чтобы оно не соскальзывало.
Очевидно, что вдоль сила \(F\) компенсирует проекцию силы тяжести на линию плоскости, которая равна \(mg\sin \alpha \), то есть по первому закону Ньютона имеем:\[F = mg\sin \alpha \]Отсюда найдем угол наклона плоскости:\[\sin \alpha = \frac{F}{{mg}}\]\[\alpha = \arcsin \left( {\frac{F}{{mg}}} \right)\]Силу упругости плоскости (она же сила реакции опоры) \(N\) легко найти так:\[N = mg\cos \alpha \]Учитывая найденный ранее угол \(\alpha\), имеем:\[N = mg\cos \left( {\arcsin \left( {\frac{F}{{mg}}} \right)} \right)\]
А как найти по этому рисунку силу трения?
Смотрите формулу (4)
Помогите плз.
Какова должна быть сила F, удерживающая брусок m=10кг на гладкой наклонной плоскости, если угол наклона плоскости a=30градусам, а сила параллельна наклонной плоскости? Считать что трение между бруском и плоскостью отсутствует. Найти силу реакции плоскости N
\[F=mg\sin \alpha\]\[N=mg\cos\alpha\]Надеюсь, посчитать сможете.
Здравствуйте
А если скорость известна 10,9 м\с, коэффициент трения 0,125, время 3с, как можно найти угол? Заранее спасибо за объяснение..
Решаете задачу абсолютно также, то есть Вы имеете:\[\upsilon = gt\left( {\sin \alpha – \mu \cos \alpha } \right)\]Откуда:\[\sin \alpha – \mu \cos \alpha = \frac{\upsilon }{{gt}}\]Выражения вида \(A\sin x – B\cos x\) приводятся к виду \(C\sin \left( {x – t} \right)\), где \(C = \sqrt {{A^2} + {B^2}} \), а \(t = {\text{arctg}}\frac{B}{A}\), поэтому:\[\sqrt {1 + {\mu ^2}} \sin \left( {\alpha – {\text{arctg}}\mu } \right) = \frac{\upsilon }{{gt}}\]\[\sin \left( {\alpha – {\text{arctg}}\mu } \right) = \frac{\upsilon }{{gt\sqrt {1 + {\mu ^2}} }}\]\[\alpha – {\text{arctg}}\mu = \arcsin \frac{\upsilon }{{gt\sqrt {1 + {\mu ^2}} }}\]\[\alpha = {\text{arctg}}\mu + \arcsin \frac{\upsilon }{{gt\sqrt {1 + {\mu ^2}} }}\]Подставляем Ваши данные:\[\alpha = {\text{arctg}}0,125 + \arcsin \frac{{10,9}}{{9,8 \cdot 3 \cdot \sqrt {1 + {{0,125}^2}} }} = 28,71^\circ \]
А если убрать коэффициент трения ?
Все очень просто, тогда ускорение будет равно:\[a = g\sin \alpha \]А скорость можно узнать по формуле:\[\upsilon = g\sin \alpha \cdot t\]
Спасибо за ответ !
помогите решить когда время составляет в конце третьей секунды.
а то я пробовал, у меня что-то не получилось
Если задача абсолютно аналогичная, то ответ будет следующий:\[\upsilon = 10 \cdot 3 \cdot \left( {\sin 30^\circ – 0,15 \cdot \cos 30^\circ } \right) = 11,1\; м/с \approx 40\; км/ч\]
Спасибо большое) оказывается цифры сошлись, ну почти))
А еще, поможете решить одну задачу?
Не перевёл в СИ!
В решении приведен также и ответ в единицах системы СИ (т.е. в м/с). Значение скорости в км/ч приведено для самопроверки с ответами в конце сборника.
В условии сказанно “в КОНЦЕ второй секунды”, не значит ли это, что нужно брать t=3?
Нет.
Например, если Вы считаете при \(t=1\) с, то получите скорость в конце первой секунды. Аналогично, если Вы считаете при \(t=2\) с, то получите скорость в конце второй секунды.
Другое дело, если бы Вас спрашивали про скорость в начале какой-то секунды, например второй. Тогда вы должны использовать \(t=1\) с.
вы пишите ” a = g * (sin?—ucos?) ” вопрос чему равен “g”
все понял
Объясните подробнее, пожалуйста, по какой теореме из геометрии вы умножаете силу тяжести на sina и cosa, когда записываете проекции
Это не теорема геометрии, это называется проецированием векторов на оси. Поищите информацию в интернете, я думаю ее там более чем предостаточно (просто в словах это проблематично объяснить, необходимо делать пояснения в виде рисунков).
А почему мы не используем силу тяги
Потому что сила тяги присутствует, например, тогда, когда работает двигатель автомобиля. В данном случае тело движется из-за силы тяжести, поэтому вводить силу тяги не имеет особого смысла.