icodepro.ruУсловие задачи:
Под каким углом к горизонту нужно бросить камень, чтобы в верхней точке траектории кинетическая энергия камня была в три раза больше его потенциальной энергии?
Задача №2.8.17 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(E_к=3E_п\), \(\alpha-?\)
Решение задачи:
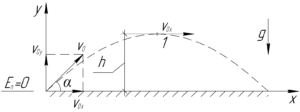В условии сказано, что \(E_к=3E_п\). Распишем кинетическую и потенциальную энергию по известным формулам:
\[\frac{{m{\upsilon^2}}}{2} = 3mgh\]
\[{\upsilon^2} = 6gh\;\;\;\;(1)\]
В верхней точке траектории скорость камня \(\upsilon\) равна проекции начальной скорости на ось \(x\):
\[\upsilon = {\upsilon _{0x}} = {\upsilon _0}\cos \alpha \;\;\;\;(2)\]
Высоту над поверхностью Земли верхней точки траектории найдем из следующей формулы кинематики:
\[0 – \upsilon _{0y}^2 = – 2gh\]
\[0 – \upsilon _0^2{\sin ^2}\alpha = – 2gh\]
\[h = \frac{{\upsilon _0^2{{\sin }^2}\alpha }}{{2g}}\;\;\;\;(3)\]
Подставим выражения (2) и (3) в (1), тогда:
\[\upsilon _0^2{\cos ^2}\alpha = 6g\frac{{\upsilon _0^2{{\sin }^2}\alpha }}{{2g}}\]
\[{\cos ^2}\alpha = 3{\sin ^2}\alpha \]
\[ctg^2 \alpha = 3\]
Учитывая, что угол броска точно меньше 90°, значит котангенс точно положительный, извлечем квадратный корень:
\[ctg \alpha = \sqrt 3 \]
\[\alpha = 30^\circ = 0,52\; рад\]
Ответ: 0,52 рад.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.16 Оконная штора массой 1 кг и длиной 2 м навертывается на валик, расположенный
2.8.18 При выстреле из орудия снаряд получил начальную скорость 300 м/с и летит
2.8.19 Телеграфный столб длиной 7 м и массой 140 кг при установке перемещается
Можно гораздо проще!!
если учесть, что:
начальная энергия = m V0^2 / 2
распределяется на кинетическую = m V^2 / 2
и
потенциальную = m g h
\(0 – \upsilon _{0y}^2 = – 2gh\)
\(0 – \upsilon _0^2{\sin ^2}\alpha = – 2gh\)
Добрый день, откуда эти формулы взялись, источник по этим формулам
Если записать закон сохранения энергии для точки бросания и верхней точки траектории, при этом скорости в этих точках разложить на проекции на оси x и y, то вы получите эту формулу.
Также, в более менее нормальном учебнике физики есть такая формула (привожу её в векторном форме):
\({\overrightarrow \upsilon ^2} – {\overrightarrow {{\upsilon _0}} ^2} = 2\overrightarrow g \cdot \overrightarrow S \)
Здесь \(\overrightarrow \upsilon\) – вектор конечной скорости, \(\overrightarrow {{\upsilon _0}}\) – вектор начальной скорости, \(\overrightarrow g\) – вектор ускорения свободного падения, \(\overrightarrow S\) – вектор перемещения.
Эта формула также работает и в соответствующих проекциях. При использовании формулы не забывайте, что в правой её части присутствует скалярное произведение векторов (не забывайте про косинус угла между векторами).