icodepro.ruУсловие задачи:
Поезд, подъезжая к станции со скоростью 60 км/ч, тормозит. За какое минимальное время он может остановиться, чтобы лежащие на полках чемоданы при коэффициенте трения 0,2 не сдвинулись с места? Торможение происходит с постоянным ускорением.
Задача №2.1.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=60\) км/ч, \(\mu=0,2\), \(t-?\)
Решение задачи:
На чемоданы действует сила трения покоя, которая равна действующей внешней силе (в данном случае это сила инерции). Максимальное значение силы трения покоя определяется законом Кулона-Амантона:
\[{F_{тр}} = \mu N\;\;\;\;(1)\]
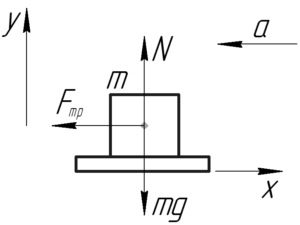
На рисунке, изображенном справа, показаны все силы, действующие на чемодан. Спроецируем все силы на оси координат и запишем второй закон Ньютона в проекциях на эти оси:
\[\left\{ \begin{gathered}
ox:{F_{тр}} = ma\;\;\;\;(2) \hfill \\
oy:N = mg \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]
Подставим (3) в (1), и полученное выражение в (2), тогда:
\[\mu mg = ma\]
\[a = \mu g\]
Время замедления легко найти по формуле определению ускорения (в ней уже учтено, что движение равнозамедленное):
\[a = \frac{{{\upsilon _0} – \upsilon }}{t}\]
Так как конечная скорость \(\upsilon = 0\) у поезда отсутствует, то:
\[a = \frac{{{\upsilon _0}}}{t} \Rightarrow t = \frac{{{\upsilon _0}}}{a}\]
В итоге конечная формула:
\[t = \frac{{{\upsilon _0}}}{{\mu g}}\]
Переведем скорость поезда в систему СИ.
\[60\; км/ч = \frac{{60 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{600}}{{36}}\; м/с = \frac{{50}}{3}\; м/с\]
Численно время до остановки равно:
\[t = \frac{{50}}{{3 \cdot 0,2 \cdot 10}} = 8,33\; с\]
Ответ: 8,33 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.11 Поезд, подъезжая к станции со скоростью 72 км/ч, начинает тормозить. Каково
2.1.13 При каком ускорении разорвется трос, прочность которого на разрыв равна
2.1.14 Груз массой 2 кг подвешен на динамометре. Снизу груз тянут с силой 10 Н
Объясните, пожалуйста, почему в формуле (1) F трения = uN, а в формуле (2) равно ma.
Дико извиняюсь за тупой вопрос. Я понял
У меня вопрос, почему в проекциях сил Fтр и ma с одинаковым знаком, хотя они противоположно направленные? И то же самое с N и mg?
Вообще, если всё подробно расписывать, то это должно выглядеть так:\[\left\{ \begin{gathered}
ox: – {F_{тр}} = – ma \hfill \\
oy: N – mg = 0 \hfill \\
\end{gathered} \right.\]Откуда Вы уже получите:\[\left\{ \begin{gathered}
ox:{F_{тр}} = ma \hfill \\
oy:N = mg \hfill \\
\end{gathered} \right.\]Я просто опускаю этот шаг, он достаточно очевиден.
Извиняюсь тогда за глупые вопросы
Не нужно извиняться, этот вопрос не глупый
Молодцы, что спрашиваете непонятные Вам вещи
почему на оси Оy записана только сила нормального давления, а по идее надо еще записать силу тяжести
N=mg
N – сила реакции опоры, mg – сила тяжести.
формула ускорения a=(V-V0)/t, а у вас a=(V0-V)/t. Объясните пожалуйста почему так
Формула a=(V-V0)/t верна для случая равноускоренного движения, здесь же имеет место равнозамедленное движение. Если вы будете работать по такой формуле, то получите отрицательное ускорение. Мне не нравится такое решение.
Я предпочитаю, когда при решении получаются положительные скорости и ускорения. Поэтому нужно находить модуль ускорения (т.е. его абсолютную величину), а его верное направление указывать на схеме.
спасибо
В дано вместо v0 стоит просто v
Исправил, спасибо