При торможении автомобиля массой 1 т скорость уменьшилась от 72 км/ч до 36 км/ч

Условие задачи:

При торможении автомобиля массой 1 т скорость уменьшилась от 72 км/ч до 36 км/ч. Какую работу совершила сила трения?

Задача №2.7.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=1\) т, \(\upsilon_0=72\) км/ч, \(\upsilon=36\) км/ч, \(A_{тр}-?\)

Решение задачи:

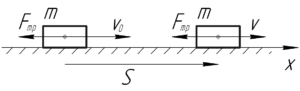Чтобы решить эту задачу, применим теорему об изменении кинетической энергии. Согласно теореме работа силы трения равна изменению кинетической энергии тела (автомобиля):

\[{A_{тр}} = \frac{{m\upsilon^2}}{2} – \frac{{m{\upsilon_0^2}}}{2}\]

\[{A_{тр}} = \frac{m}{2}\left( {\upsilon^2 – {\upsilon_0^2}} \right)\]

Переведем массу автомобиля и скорости в единицы системы СИ:

\[1\;т = 1000\;кг\]

\[72\;км/ч = \frac{{72 \cdot 1000}}{{1 \cdot 3600}}\;м/с = 20\;м/с\]

\[36\;км/ч = \frac{{36 \cdot 1000}}{{1 \cdot 3600}}\;м/с = 10\;м/с\]

Посчитаем ответ:

\[{A_{тр}} = \frac{{1000}}{2}\left( {{{10}^2} – {{20}^2}} \right) =  – 150000\;Дж =  – 0,15\;МДж\]

Неудивительно, что работа силы трения отрицательна, ведь её вектор направлен против перемещения автомобиля.

Ответ: -0,15 МДж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.7.11 Во сколько раз изменится запас потенциальной энергии упруго деформированного тела
2.7.13 Автомобиль массой 1500 кг, двигаясь равноускоренно, проходит путь 20 м за 2 с
2.7.14 На какой высоте над поверхностью Луны тело будет обладать такой же потенциальной