Решение: С какой минимальной силой, направленной горизонтально, нужно прижать плоский

Условие задачи:

С какой минимальной силой, направленной горизонтально, нужно прижать плоский брусок массой 5 кг к вертикальной плоскости, чтобы он не соскользнул вниз? Коэффициент трения между бруском и стеной 0,1.

Задача №2.1.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=5\) кг, \(\mu=0,1\), \(F-?\)

Решение задачи:

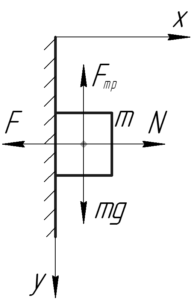Изобразим на схеме плоский брусок и силы, действующие на него: это искомая сила \(F\), сила нормальной реакции опоры \(N\), сила тяжести \(mg\) и сила трения покоя \(F_{тр}\). Так как брусок не движется, то запишем первый закон Ньютона в проекции на оси декартовой системы координат.

\[\left\{ \begin{gathered}
ox:F = N \;\;\;\;(1)\hfill \\
oy:mg = {F_{тр}} \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]

Сила трения покоя равна внешней силе, приложенной к бруску (это и видно из выражения (2)), но не превышает силы трения скольжения:

\[{F_{тр}} \leq \mu N\]

Условие же минимальности силы \(F\) соответствует тому крайнему случаю, когда сила трения покоя уже равна силе трения скольжения, но тело ещё не движется.

\[{F_{тр}} = \mu N\]

Подставим эту формулу в выражение (2).

\[mg = \mu N \Rightarrow N = \frac{{mg}}{\mu }\]

Из выражения (1) следует:

\[F = \frac{{mg}}{\mu }\]

Подставим численные данные задачи в дробь и посчитаем нужный нам ответ.

\[F = \frac{{5 \cdot 10}}{{0,1}} = 500\; Н = 0,5\; кН\]