Условие задачи:
С какой начальной скоростью \(\upsilon_0\) нужно бросить вниз мяч с высоты \(h\), чтобы он подпрыгнул на высоту \(2h\)? Трением о воздух и другими потерями механической энергии пренебречь.
Задача №2.8.32 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(h\), \(2h\), \(\upsilon_0-?\)
Решение задачи:
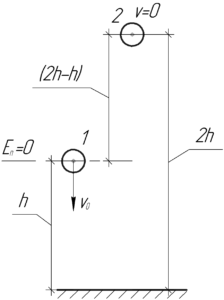 Благодаря последнему предложению из условия задачи, мы можем воспользоваться законом сохранения энергии, согласно которому полная механическая энергия мяча должна сохраняться.
Благодаря последнему предложению из условия задачи, мы можем воспользоваться законом сохранения энергии, согласно которому полная механическая энергия мяча должна сохраняться.
Выберем уровень нуля потенциальной энергии на высоте \(h\). Понятно, что при таком выборе в начале у мяча на высоте \(h\) (точка 1) имелась только кинетическая энергия, а после отскока от земли на высоте \(2h\) (точка 2) — только потенциальная. Используя всем знакомые формулы, запишем:
\[\frac{{m\upsilon _0^2}}{2} = mg\left( {2h — h} \right)\]
\[\frac{{m\upsilon _0^2}}{2} = mgh\]
\[{\upsilon _0} = \sqrt {2gh} \]
Ответ: \(\sqrt {2gh}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.31 Пуля, летящая горизонтально со скоростью 400 м/с, попадает в ящик, лежащий
2.8.33 Шарик массой m, подвешенный на нити, отклонен от положения равновесия на угол
2.8.34 Шарик подбросили вверх, сообщив ему кинетическую энергию 20 Дж. Через

 icodepro.ru
icodepro.ru
Как решить методом кинематики?
Где взяли 9,8м/с?
Не понял вопроса
Это ускорение свободного падения 9,8 м/с^2, но иногда можно записать с погрешностью, округлив до 10.
Ааааа, вот о чем был вопрос

Обычно наоборот спрашивают, откуда взяли 10, а тут вопрос про 9,8.
Да и где в решении у меня численные данные, в задаче же их нет