icodepro.ruУсловие задачи:
Самолет для взлета должен иметь скорость 25 м/с. Длина пробега перед взлетом 100 м. Масса самолета 1000 кг, коэффициент сопротивления равен 0,02. Какова мощность моторов в момент взлета, если движение равноускоренное?
Задача №2.7.33 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon=25\) м/с, \(S=100\) м, \(m=1000\) кг, \(k=0,02\), \(N-?\)
Решение задачи:
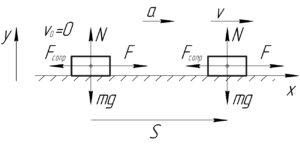Мгновенную мощность моторов \(N\) перед взлетом найдем из формулы:
\[N = F \cdot \upsilon \;\;\;\;(1)\]
Чтобы найти силу тяги \(F\), запишем второй закон Ньютона в проекции на ось \(x\):
\[F – {F_{сопр}} = ma\]
Сила сопротивления \(F_{сопр}\) равна произведению коэффициента сопротивления \(k\) на силу нормальной реакции опоры \(N\):
\[{F_{сопр}} = kN\]
Первый закон Ньютона, записанный в проекции на ось \(y\) даст такое равенство:
\[N = mg\]
\[{F_{сопр}} = kmg\]
Значит:
\[F – kmg = ma\]
\[F = m\left( {a + kg} \right)\;\;\;\;(2)\]
Ускорение самолета найдем по следующей формуле из кинематики (понятно, что начальная скорость самолета равна нулю):
\[{\upsilon ^2} = 2aS\]
\[a = \frac{{{\upsilon ^2}}}{{2S}}\;\;\;\;(3)\]
Подставим (3) в (2), а полученное – в формулу (1). В итоге имеем:
\[N = m\left( {\frac{{{\upsilon ^2}}}{{2S}} + kg} \right) \cdot \upsilon \]
Подставив исходные данные задачи в формулу, посчитаем ответ:
\[N = 1000 \cdot \left( {\frac{{{{25}^2}}}{{2 \cdot 100}} + 0,02 \cdot 10} \right) \cdot 25 = 83125\;Вт \approx 83\;кВт\]
Ответ: 83 кВт.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.7.32 Резец токарного станка мощностью 3 кВт снимает в минуту стружку длиной 500 мм
2.7.34 Тело массой 1 кг, брошенное с вышки в горизонтальном направлении со скоростью
2.7.35 Тепловоз за 5 мин набирает скорость 72 км/ч. Определить среднюю мощность
все супер!!!
Самолет массой P = 231 кН должен развивать скорость v = 85 м / с, чтобы иметь возможность взлететь.
Двигатель реактивного самолета может создавать максимальную силу F = 107 кН, но этого недостаточно, чтобы самолет достиг скорости, необходимой для взлета на взлетно-посадочной полосе длиной d = 90 м, например на авианосце.
Какая минимальная (постоянная) сила должна быть приложена к самолету пусковой установкой, используемой для облегчения взлета самолетов?
Предположим, что и пусковая установка, и двигатель самолета оказывают на самолет постоянную силу на протяжении всего его ускорения на 90-метровой взлетно-посадочной полосе.
a = v^2 – 0^2/2d a = 18.06m/с^2
F = m(a + g)
m = 23555.4кг
23555,4(18,06 + 10) = 660965,524Н
660,9kН – 107kН = 553.9kН
помогите пожалуйста, я правильно решаю или нет? у меня не указан коэффициент сопротивленияпоэтому я его нигде не учитываю
Необходимое ускорение Вы определяете правильно:\[a = \frac{{{\upsilon ^2}}}{{2d}}\]Далее Вам нужно записать второй закон Ньютона в проекции на горизонтальную ось:\[F + {F_у} = ma\]Зная вес \(P\), найдем массу самолета:\[m = \frac{P}{g}\]Тогда:\[F + {F_у} = \frac{P}{g}a\]\[F + {F_у} = \frac{{P{\upsilon ^2}}}{{2dg}}\]\[{F_у} = \frac{{P{\upsilon ^2}}}{{2dg}} – F\]\[{F_у} = \frac{{231 \cdot {{10}^3} \cdot {{85}^2}}}{{2 \cdot 90 \cdot 9,81}} – 107 \cdot {10^3} = 838,2 \cdot {10^3} = 838,2\;кН\]
Откуда Вы взяли F = m(a + g)?
41,5 кВт это правильный ответ
И где тогда ошибка в решении?
зная ускорение и путь мы можем найти время, если подставить в классическую формулу нахождения мощности получим эти цифры.
Вы так найдете среднюю мощность, а в условии просят найти, цитирую, “мощность моторов в момент взлета”.
решение замечательное. все просто и понятно. спасибо
Всегда пожалуйста! Спасибо за Ваш отзыв, он нам очень важен!