Санки можно удержать на ледяной горке с уклоном 0,2 (отношение высоты к длине)

Условие задачи:

Санки можно удержать на ледяной горке с уклоном 0,2 (отношение высоты к длине) силой, параллельной горке и не меньшей 49 Н. Чтобы тянуть санки в горку равномерно, силу надо увеличить на 9,8 Н. С каким ускорением будут двигаться санки, если им предоставить возможность скатываться?

Задача №2.3.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(tg \alpha = 0,2\), \(F=49\) Н, \(\Delta F=9,8\) Н, \(a-?\)

Решение задачи:

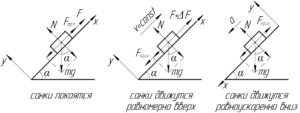Для всех трёх случаев нарисуем схемы, на которых покажем все силы, действующие на санки.

В первом случае санки покоятся, так как удерживаются силой \(F\) и силой трения покоя. Запишем первый закон Ньютона в проекции на ось \(x\) и \(y\):

\[\left\{ \begin{gathered}
F + {F_{тр.п}} – mg \cdot \sin \alpha = 0 \hfill \\
N = mg \cdot \cos \alpha \hfill \\
\end{gathered} \right.\]

Сила трения покоя принимает в данном случае максимальное значение, т.е. она уже равно силе трения скольжения, но санки не соскальзывают. Именно поэтому в условии пишут, что “санки можно удержать силой не меньшей 49 Н”.

\[{F_{тр.п}} = \mu N\]

\[{F_{тр.п}} = \mu mg \cdot \cos \alpha \]

Тогда:

\[F + \mu mg \cdot \cos \alpha  – mg \cdot \sin \alpha  = 0\;\;\;\;(1)\]

Также выразим \(F\), это пригодится нам в дальнейшем решении:

\[F = mg \cdot \sin \alpha  – \mu mg \cdot \cos \alpha \;\;\;\;(2)\]

Во втором случае санки движутся вверх равномерно. Опять запишем первый закон Ньютона в проекции на обе оси:

\[\left\{ \begin{gathered}
F + \Delta F – {F_{тр.ск}} – mg \cdot \sin \alpha = 0 \hfill \\
N = mg \cdot \cos \alpha \hfill \\
\end{gathered} \right.\]

Обратите внимание, что в данном случае имеет место сила трения скольжения. Она равна максимальной силе трения покоя, определенной в первом случае, поэтому:

\[F + \Delta F – \mu mg \cdot \cos \alpha  – mg \cdot \sin \alpha  = 0\;\;\;\;(3)\]

Вычтем из равенства (3) равенство (1), тогда:

\[\Delta F – 2\mu mg \cdot \cos \alpha  = 0\]

\[\mu mg \cdot \cos \alpha  = \frac{{\Delta F}}{2}\]

Полученное подставим в (1), далее выразим массу санок:

\[F + \frac{{\Delta F}}{2} – mg \cdot \sin \alpha  = 0\]

\[m = \frac{{2F + \Delta F}}{{2g \cdot \sin \alpha }}\;\;\;\;(4)\]

В третьем случае санки скользят равноускоренно вниз, применим второй закон Ньютона в проекции на ось \(x\):

\[mg \cdot \sin \alpha  – {F_{тр.ск}} = ma\]

Аналогично вышеприведенному находим силу трения скольжения, тогда:

\[mg \cdot \sin \alpha  – \mu mg \cdot \cos \alpha  = ma\]

\[a = \frac{{mg \cdot \sin \alpha  – \mu mg \cdot \cos \alpha }}{m}\]

Числитель дроби в правой части равен \(F\) (смотрите формулу (2)), а вместо массы в знаменателе подставим (4):

\[a = \frac{{2Fg\sin \alpha }}{{2F + \Delta F}}\]

Необходимо синус угла выразить через данный в условии тангенс угла, для этого воспользуемся следующей формулой:

\[\sin \alpha = \frac{{tg\alpha }}{{\sqrt {1 + {tg^2}\alpha } }}\]

Окончательно получим:

\[a = \frac{{2Fg}}{{2F + \Delta F}} \cdot \frac{{tg\alpha }}{{\sqrt {1 + {tg^2}\alpha } }}\]

Посчитаем ответ:

\[a = \frac{{2 \cdot 49 \cdot 10}}{{2 \cdot 49 + 9,8}} \cdot \frac{{0,2}}{{\sqrt {1 + {{0,2}^2}} }} = 1,78\; м/с^2\]

Ответ: 1,78 м/с².

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.3.4 По наклонной плоскости с углом наклона 30 градусов к горизонту скользит вниз тело
2.3.6 Тело массой 1 кг, имеющее у основания наклонной плоскости скорость 6 м/с
2.3.7 Тело скользит равномерно по наклонной плоскости, угол наклона которой 30 градусов