Условие задачи:
Шарик массой 100 г упал с высоты 2,5 м на горизонтальную плиту, масса которой много больше масса шарика и отскочил от неё вверх. Считая удар упругим, определить импульс, полученный плитой.
Задача №2.9.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=100\) г, \(h=2,5\) м, \(M \gg m\), \(p-?\)
Решение задачи:
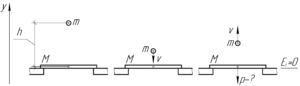 Если пренебречь сопротивлением воздуха, то из закона сохранения энергии можно определить скорость шарика непосредственно перед упругим ударом о плиту:
Если пренебречь сопротивлением воздуха, то из закона сохранения энергии можно определить скорость шарика непосредственно перед упругим ударом о плиту:
\[mgh = \frac{{m{\upsilon ^2}}}{2}\]
\[\upsilon = \sqrt {2gh} \;\;\;\;(1)\]
Если удар происходит очень быстро, то можно применить закон сохранения импульса для момента непосредственно до и сразу после удара в проекции на ось \(y\).
\[- m\upsilon = m\upsilon – p\]
\[p = 2m\upsilon \]
Используя (1), получим решение задачи в общем виде:
\[p = 2m\sqrt {2gh} \]
Подставим численные данные задачи в формулу и посчитаем ответ:
\[p = 2 \cdot 0,1\sqrt {2 \cdot 10 \cdot 2,5} = 1,41\; Н \cdot с\]
Интересно, что плита получит импульс, но поскольку её масса велика, то скорость плиты после удара настолько мала, что ею можно пренебречь.
Ответ: 1,41 Н·с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.9.1 Тело массой 1 кг упруго ударяется о покоящееся тело массой 3 кг и летит обратно
2.9.3 Во сколько раз уменьшится энергия нейтрона n при столкновении с ядром углерода C
2.9.4 Гранату бросают от поверхности земли под углом 30 градусов к горизонту

 icodepro.ru
icodepro.ru
т.е. получается, что скорость до взаимодействия с плитой равная V и сразу после удара и, соответственно, отскока равна также V?
Если удар упругий (а об этом сказано в условии), то да – скорость до удара равна численно скорости после удара