icodepro.ruУсловие задачи:
Шарик подлетает к неподвижной вертикальной стенке сверху со скоростью 10 м/с под углом \(\alpha=45^\circ\) к стенке. Найти тангенс угла, под которым шарик отскочит от стенки (угол также отсчитывается от стенки). Длительность удара 50 мс.
Задача №2.9.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=10\) м/с, \(\alpha=45^\circ\), \(t=50\) мс, \(tg \beta – ?\)
Решение задачи:
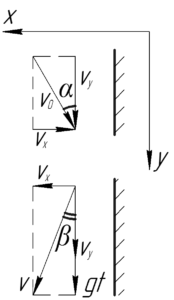Введем взаимно перпендикулярные оси, причем ось \(x\) направим перпендикулярно к стенке, а ось \(y\) – вдоль стенки (смотрите рисунок).
Вдоль оси \(x\) на шарик действует сила реакция со стороны стенки, но поскольку мы никак не можем узнать её среднюю величину за время удара, примем, что после удара проекция скорости на эту ось останется такой же по величине, разве что поменяет направление.
Вдоль же оси \(y\) действует сила тяжести. Так как удар длился какое-то время \(t\), то проекция скорости шарика на эту ось увеличится на величину \(gt\).
Тогда искомый тангенс угла отскока равен:
\[tg\beta = \frac{{{\upsilon _0}\sin \alpha }}{{{\upsilon _0}\cos \alpha + gt}}\]
Переведем длительность удара в систему СИ.
\[50\; мс = 50 \cdot {10^{ – 3}}\; с = 0,05\; с\]
Считаем численный ответ к задаче, подставив исходные данные в формулу.
\[tg\beta = \frac{{10 \cdot \sin 45^\circ }}{{10 \cdot \cos 45^\circ + 10 \cdot 0,05}} = 0,93\]
Ответ: 0,93.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.9.5 Два упругих стальных шара массами m1=0,2 кг и m2=0,1 кг подвешены рядом
2.9.7 На горизонтальной поверхности в 3 м от вертикальной стенки находится шар массой
2.10.1 По абсолютно гладкой поверхности движется со скоростью 6 м/с ящик с песком
В решение нет такого ответа
Есть варианты 43, 55, 45, 30, 60
Вероятно в Вашей задаче просят найти величину самого угла, а не тангенса этого угла, в таком случае правильный ответ 43°
“Вдоль же оси y действует сила тяжести. Так как удар длился какое-то время t, то проекция скорости шарика на эту ось увеличится на величину gt”. Почему проекция скорости шарика на эту ось увеличится величину gt ? Из какого закона это вытекает и почему ?
Думаю ты знаешь такую формулу:
Δp=F*Δt (1)
Она выводится из второго закона Ньютона, если записать его в виде, в котором его и вывел Ньютон:
F=Δp/Δt
Запишем формулу (1) в проекции на ось y, учитывая, что вдоль оси y действует только сила тяжести, тогда будем иметь:
Δp_y=mg*Δt (1)
Из формулы видно, что импульс (а значит и скорость) зависит от длительности действия силы. Если учесть, что Δp_y=m*Δv_y, то:
Δv=g*Δt (1)
Смотри, обычно в задачах на удары считается, что удар происходит мгновенно, то есть длительность удара равна 0. Поэтому в таких задачах проекция скорости на ось y за удар не меняется, а угол падения равен углу отражения.
Но тут мы имеем другой случай, здесь это изменение нужно учесть.
Спасибо, хорошо объясняете.
Вы записали второй закон Ньютона через изменение импульса, где F – равнодействующая. Но в момент удара (на протяжении 50 мс) на него действует не только сила тяжести, но и сила реакции опоры (которая будет меняться со временем). Вы пишете, что вдоль ОХ на тело не действует силы, но это не так. Если бы на него не действовали силы по оси ОХ, то тогда и не было бы изменения импульс по ОХ, а он есть. Поэтому ваше решение не учитывает влияние силы реакции опоры (которую тут, конечно, нужно брать средней).
Да, Вы верно подметили, спасибо за ценный комментарий.
Поскольку никаких сведений о силе реакции со стороны стенки в задаче не дано, будем считать, что проекция скорости на ось \(x\) просто изменит свое направление на противоположное, иначе задача при текущих данных не может быть решена