Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с

Условие задачи:

Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 1 м/с, второго – 2 м/с. Сколько энергии превратилась в тепло после абсолютно неупругого удара шаров?

Задача №2.10.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=1\) кг, \(M=2\) кг, \(\upsilon_0=1\) м/с, \(u_0=2\) м/с, \(Q-?\)

Решение задачи:

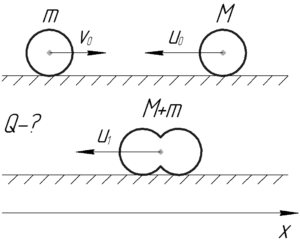Как обычно это делается в задачах на абсолютно неупругий удар, запишем закон сохранения импульса (ЗСИ) в проекции на ось \(x\) и закон сохранения энергии (ЗСЭ):

\[\left\{ \begin{gathered}
– M{u_0} + m{\upsilon _0} = – \left( {M + m} \right){u_1} \;\;\;\;(1)\hfill \\
\frac{{m\upsilon _0^2}}{2} + \frac{{Mu_0^2}}{2} = \frac{{\left( {M + m} \right)u_1^2}}{2} + Q \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]

Из равенства (1) выразим скорость тел \(u\) после удара:

\[{u_1} = \frac{{M{u_0} – m{\upsilon _0}}}{{M + m}}\]

Полученное выражение подставим в (2):

\[\frac{{m\upsilon _0^2}}{2} + \frac{{Mu_0^2}}{2} = \frac{{\left( {M + m} \right)}}{2} \cdot \frac{{{{\left( {M{u_0} – m{\upsilon _0}} \right)}^2}}}{{{{\left( {M + m} \right)}^2}}} + Q\]

Оставим искомую теплоту \(Q\) в правой части, а все остальное перенесем в левую.

\[Q = \frac{{m\upsilon _0^2}}{2} + \frac{{Mu_0^2}}{2} – \frac{{{{\left( {M{u_0} – m{\upsilon _0}} \right)}^2}}}{{2\left( {M + m} \right)}}\]

Приведем под общий знаменатель:

\[Q = \frac{{m\upsilon _0^2\left( {M + m} \right) + Mu_0^2\left( {M + m} \right) – {{\left( {M{u_0} – m{\upsilon _0}} \right)}^2}}}{{2\left( {M + m} \right)}}\]

Раскроем скобки в числителе:

\[Q = \frac{{mM\upsilon _0^2 + {m^2}\upsilon _0^2 + {M^2}u_0^2 + mMu_0^2 – {M^2}u_0^2 + 2mM{u_0}{\upsilon _0} – {m^2}\upsilon _0^2}}{{2\left( {M + m} \right)}}\]

\[Q = \frac{{mM\upsilon _0^2 + mMu_0^2 + 2mM{u_0}{\upsilon _0}}}{{2\left( {M + m} \right)}}\]

\[Q = \frac{{mM\left( {\upsilon _0^2 + 2{u_0}{\upsilon _0} + u_0^2} \right)}}{{2\left( {M + m} \right)}}\]

\[Q = \frac{{mM{{\left( {{\upsilon _0} + {u_0}} \right)}^2}}}{{2\left( {M + m} \right)}}\]

Задача решена в общем виде. Поскольку все численные данные приведены в системе СИ, то можно приступать к вычислению ответа.

\[Q = \frac{{1 \cdot 2 \cdot {{\left( {1 + 2} \right)}^2}}}{{2\left( {2 + 1} \right)}} = 3\; Дж\]

Ответ: 3 Дж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.6 Два шара массами 0,3 и 0,2 кг движутся навстречу друг другу. Скорость первого шара
2.10.7 Охотник стреляет с легкой надувной лодки, находящейся в покое. Какую скорость