Снаряд, выпущенный из пушки под углом 45 градусов к горизонту, разрывается

Условие задачи:

Снаряд, выпущенный из пушки под углом 45° к горизонту, разрывается в верхней точке траектории на два осколка равной массы. Первый осколок через 20 с падает прямо под точкой разрыва. На каком расстоянии от первого осколка упадет второй осколок, если разрыв произошёл на высоте 2 км?

Задача №2.10.36 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=45^\circ\), \(t=20\) с, \(H=2\) км, \(L-?\)

Решение задачи:

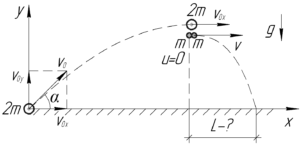Нам неизвестна начальная скорость снаряда, но известна высота \(H\) наивысшей точки его подъема. Запишем такую формулу кинематики (здесь \(\upsilon_0 \sin \alpha\) – это проекция начальной скорости на ось \(y\)):

\[0 – \upsilon _0^2{\sin ^2}\alpha  =  – 2gH\]

Выразим начальную скорость \(\upsilon_0\):

\[{\upsilon _0} = \frac{{\sqrt {2gH} }}{{\sin \alpha }}\;\;\;\;(1)\]

В верхней точке траектории снаряд взрывается, при этом первый осколок падает прямо под точкой разрыва. Что это означает? То, что проекция скорости первого осколка \(u\) после взрыва на ось \(x\) равна нулю, иначе бы он не упал бы прямо под точкой разрыва. Найдем проекцию этой скорости на ось \(y\), записав уравнение движения первого осколка в проекции на вертикальную ось.

\[H = ut + \frac{{g{t^2}}}{2}\]

\[u = \frac{H}{t} – \frac{{gt}}{2}\]

Давайте посчитаем численное значение скорости первого осколка \(u\) после взрыва. Конечно, мы так отойдем от цели решить задачу в общем виде, но в этой задаче это действие чрезвычайно важно.

\[u = \frac{{2 \cdot {{10}^3}}}{{20}} – \frac{{10 \cdot 20}}{2} = 0\; м/с\]

Внимание! Первый осколок после взрыва не имеет вообще никакой скорости! Это очень упрощает нашу задачу. В момент взрыва импульс снаряда направлен горизонтально (как и скорость). Так как после взрыва первый осколок не имеет скорости (а значит и импульса), то импульс второго осколка должен быть направлен также горизонтально. Давайте запишем закон сохранения импульса в проекции на ось \(x\) в верхней точке до и после взрыва:

\[2m{\upsilon _0}\cos \alpha  = m \upsilon \]

\[\upsilon  = 2{\upsilon _0}\cos \alpha \;\;\;\;(2)\]

Здесь \(2m\) – это масса снаряда, \(m\) – это масса осколков.

Теперь обратите внимание на тот факт, что первый осколок, “брошенный” без начальной скорости, и второй осколок, “брошенный” горизонтально, с одной высоты будут падать одинаковое данное время \(t\). Тогда легко найти расстояние, пройденное вторым осколком по горизонтали, т.е. по сути искомое расстояние \(L\), по следующей формуле:

\[L = \upsilon t\;\;\;\;(3)\]

Подставим (1) в (2), а полученное подставим в (3), тогда получим:

\[L = 2\frac{{\sqrt {2gH} }}{{\sin \alpha }}\cos \alpha  \cdot t\]

\[L = 2\sqrt {2gH}  \cdot ctg \alpha  \cdot t\]

Посчитаем численный ответ, предварительно переведя высоту в систему СИ:

\[2\; км = 2000\; м\]

\[L = 2\sqrt {2 \cdot 10 \cdot 2000}  \cdot ctg 45^\circ  \cdot 20 = 8000\; м\]

Ответ: 8000 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.10.35 С незакрепленной горки (клина) массой 1 кг соскальзывает тело массой 500 г. Угол
2.10.37 Человек, сидящий в лодке, бросает камень под углом 60 градусов к горизонту. Масса
2.1.1 Тело движется прямолинейно под действием силы 16 Н. Зависимость пути от времени