Решение: Спортивный молот - ядро на тросике длиной L, бросают, раскрутив вокруг себя

Условие задачи:

Спортивный молот – ядро на тросике длиной \(L\), бросают, раскрутив вокруг себя с большой скоростью. Найти максимальное расстояние, которое может пролететь молот. Натяжение тросика перед броском в \(N\) раз превышает силу тяжести молота, \(N \gg 1\).

Задача №2.4.33 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(L\), \(T=Nmg\), \(N \gg 1\), \(S_{max}-?\)

Решение задачи:

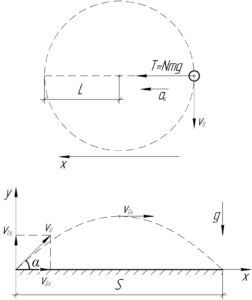На ядро действуют две силы – сила натяжения тросика \(T\) и сила тяжести \(mg\). Мы не знаем как расположена в пространстве плоскость вращения спортивного молота, но поскольку в условии сказано, что сила натяжения в \(N\) раз больше силы тяжести, причем \(N \gg 1\), то проекцией силы тяжести на ось \(x\), параллельной центростремительному ускорению \(a_ц\), можно пренебречь. Тогда второй закон Ньютона в проекции на ось \(x\) запишется в следующем виде:

\[T = m{a_ц}\;\;\;\;(1)\]

Если скорость ядро сразу перед броском равна \(\upsilon_0\), то центростремительное ускорение можно найти по формуле:

\[{a_ц} = \frac{{\upsilon _0^2}}{L}\]

Так как по условию \(T=Nmg\), то равенство (1) примет вид:

\[Nmg = m\frac{{\upsilon _0^2}}{L}\]

\[\upsilon _0^2 = NgL\;\;\;\;(2)\]

Теперь разберемся с движением ядра после броска. Пусть в момент броска вектор начальной скорости ядра \(\upsilon_0\) составляет с горизонтом угол \(\alpha\). Тогда дальность полета можно определить по формуле:

\[S = {\upsilon _0} \cdot \cos \alpha \cdot 2t\]

Здесь \(t\) – это время движения ядра до высшей точки траектории. Его можно найти по формуле:

\[t = \frac{{{\upsilon _0} \cdot \sin \alpha }}{g}\]

Тогда:

\[S = {\upsilon _0} \cdot \cos \alpha \cdot 2 \cdot \frac{{{\upsilon _0} \cdot \sin \alpha }}{g}\]

\[S = \frac{{\upsilon _0^2 \cdot \sin 2\alpha }}{g}\]

Понятно, что угол \(\alpha\) лежит в диапазоне от 0° до 90°. При этом максимальная дальность полета спортивного снаряда имеет место при угле \(\alpha=45^\circ\).

\[{S_{max}} = \frac{{\upsilon _0^2}}{g}\]

Учитывая ранее полученное выражение (2) для квадрата скорости, имеем:

\[{S_{max}} = \frac{{NgL}}{g}\]

\[{S_{max}} = NL\]

Задача решена в общем виде.