Решение: Стержень длины L движется по гладкой горизонтальной поверхности. Какая упругая

Условие задачи:

Стержень длины \(L\) движется по гладкой горизонтальной поверхности. Какая упругая сила возникает в сечении стержня на расстоянии \(L/4\) от конца, к которому приложена сила \(F\), направленная вдоль стержня?

Задача №2.1.83 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(L\), \(\frac{L}{4}\), \(F\), \(T-?\)

Решение задачи:

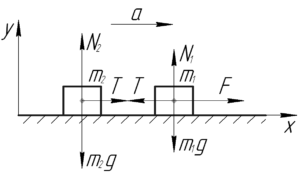Чтобы найти силу, возникающую в некотором сечении стержня, перейдем к следующей эквивалентной схеме. Представим первые \(L/4\) м стержня в виде бруска массы \(m_1\), к которому приложена сила \(F\). Остальные \(3L/4\) м стержня представим в виде другого бруска массы \(m_2\), который соединен с первым посредством невесомой нерастяжимой нити. Сила натяжения этой нити равна по величине искомой упругой силе, возникающей в заданном сечении.

Пусть масса всего стержня \(m\). Так как масса распределена по длине стержня равномерно, то масса брусков, о которых говорится выше, равна соответственно:

\[\left\{ \begin{gathered}
{m_1} = \frac{m}{4} \hfill \\
{m_2} = \frac{{3m}}{4} \hfill \\
\end{gathered} \right.\]

Поверхность, по которой скользит стержень, гладкая, значит силы трения отсутствуют. Запишем второй закон Ньютона для брусков в проекции на ось \(x\). Очевидно, что бруски двигаются с одинаковым ускорением (таким же, как и стержень).

\[\left\{ \begin{gathered}
F – T = {m_1}a \hfill \\
T = {m_2}a \hfill \\
\end{gathered} \right.\]

Сложим вместе оба этих выражения.

\[F = \left( {{m_1} + {m_2}} \right)a\]

\[a = \frac{F}{{{m_1} + {m_2}}}\]

Подставим полученную формулу для ускорения в последнее выражение системы.

\[T = \frac{{F{m_2}}}{{{m_1} + {m_2}}}\]

Понятно, что \({m_1} + {m_2} = m\). Выше было сказано, что \({m_2} = \frac{{3m}}{4}\). Учитывая все это:

\[T = \frac{{3Fm}}{{4m}} = \frac{{3F}}{4}\]