icodepro.ruУсловие задачи:
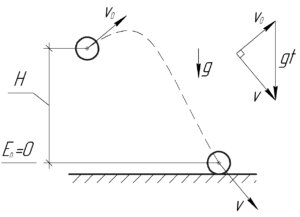
Тело, брошенное с вышки высотой 10 м, упало на землю со скоростью 15 м/с, направленной под прямым углом к начальной скорости. Определить время падения.
Задача №2.8.36 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(H=10\) м, \(\upsilon=15\) м/с, \(\alpha=90^\circ\), \(t-?\)
Решение задачи:
Из кинематики известно, что:
\[\overrightarrow \upsilon = \overrightarrow {{\upsilon _0}} + \overrightarrow g t\]
Учитывая, что между скоростями угол равен 90°, то нарисуем соответствующий треугольник скоростей. По теореме Пифагора справедливо следующее выражение:
\[{\upsilon ^2} + \upsilon _0^2 = {g^2}{t^2}\]
Выразим отсюда искомое время падения \(t\):
\[t = \frac{1}{g}\sqrt {{\upsilon ^2} + \upsilon _0^2} \;\;\;\;(1)\]
Поскольку потерь энергии нет, то воспользуемся законом сохранения энергии:
\[mgH + \frac{{m\upsilon _0^2}}{2} = \frac{{m{\upsilon ^2}}}{2}\]
Выразим из этого выражения квадрат начальной скорости:
\[\upsilon _0^2 = {\upsilon ^2} – 2gH\;\;\;\;(2)\]
Подставим (2) в (1):
\[t = \frac{1}{g}\sqrt {{\upsilon ^2} + {\upsilon ^2} – 2gH} \]
\[t = \frac{1}{g}\sqrt {2{\upsilon ^2} – 2gH} \]
Мы получили решение задачи в общем виде. Теперь посчитаем численный ответ.
\[t = \frac{1}{{10}}\sqrt {2 \cdot {{15}^2} – 2 \cdot 10 \cdot 10} = 1,58\; с\]
Ответ: 1,58 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.35 Мяч падает с высоты 7,5 м на гладкий пол. Какую скорость нужно сообщить мячу
2.8.37 Мяч скатился с горы высотой 20 м и после короткого горизонтального участка упал
2.8.38 Пуля массой 9 г, летевшая вертикально вверх со скоростью 200 м/с, пробила
