Условие задачи:

Тело массой 1 кг упруго ударяется о покоящееся тело массой 3 кг и летит обратно. Найти долю потерянной при этом первым телом кинетической энергии.

Задача №2.9.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$m=1$ кг, $M=3$ кг, $\frac{E_2}{E_1}-?$

Решение задачи:

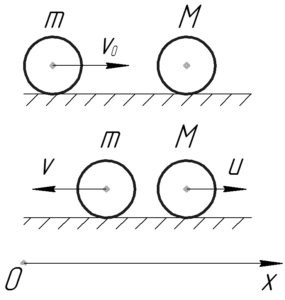Так как тела ударяются упруго, то потерянная первым телом кинетическая энергия равна кинетической энергии второго тела после удара. Поэтому искомое отношение можно записать в таком виде:

$$\frac{{{E_2}}}{{{E_1}}} = \frac{{M{u^2} \cdot 2}}{{2 \cdot m{\upsilon_0 ^2}}} = \frac{{M{u^2}}}{{m{\upsilon_0 ^2}}} = \frac{M}{m}{\left( {\frac{u}{\upsilon_0 }} \right)^2} \;\;\;\;(1)$$

Теперь выполним классические для всех подобных задач действия: запишем закон сохранения импульса в проекции на ось $x$ и закон сохранения энергии.

$$\left\{ \begin{gathered} m{\upsilon _0} = — m\upsilon + Mu \;\;\;\;(2)\hfill \\ \frac{{m\upsilon _0^2}}{2} = \frac{{m{\upsilon ^2}}}{2} + \frac{{M{u^2}}}{2} \;\;\;\;(3)\hfill \\ \end{gathered} \right.$$

Равенство (2) запишем в виде:

$$m\left( {{\upsilon _0} + \upsilon } \right) = Mu\;\;\;\;(4)$$

В равенстве (3) домножим обе части на 2, далее перенесем все члены с $m$ в левую часть и вынесем $m$ за скобки:

$$m\left( {\upsilon _0^2 — {\upsilon ^2}} \right) = M{u^2}$$

Распишем разность квадратов в левой части этого равенства:

$$m\left( {{\upsilon _0} + \upsilon } \right)\left( {{\upsilon _0} — \upsilon } \right) = M{u^2}$$

Используя (4), получим:

$$Mu\left( {{\upsilon _0} — \upsilon } \right) = M{u^2}$$

$$u = {\upsilon _0} — \upsilon \;\;\;\;(5)$$

Откуда имеем:

$$\upsilon = {\upsilon _0} — u$$

Подставим это выражение в равенство (2), тогда получим:

$$m{\upsilon _0} = — m\left( {{\upsilon _0} — u} \right) + Mu$$

$$m{\upsilon _0} = — m{\upsilon _0} + mu + Mu$$

$$2m{\upsilon _0} = u\left( {M + m} \right)$$

Окончательно получим:

$$u = \frac{{2m{\upsilon _0}}}{{m + M}}$$

В итоге формула (1) примет вид:

$$\frac{{{E_2}}}{{{E_1}}} = \frac{M}{m}{\left( {\frac{{2m{\upsilon _0}}}{{{\upsilon _0}\left( {m + M} \right)}}} \right)^2} = \frac{M}{m}{\left( {\frac{{2m}}{{\left( {m + M} \right)}}} \right)^2}$$

$$\frac{{{E_2}}}{{{E_1}}} = \frac{{4Mm}}{{{{\left( {m + M} \right)}^2}}}$$

Остается только посчитать ответ к этой задаче:

$$\frac{{{E_2}}}{{{E_1}}} = \frac{{4 \cdot 3 \cdot 1}}{{{{\left( {1 + 3} \right)}^2}}} = 0,75$$

Ответ: 0,75.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.53 Шарик на нити отклонили от вертикали на 60 градусов и отпустили без начальной
2.9.2 Шарик массой 100 г упал с высоты 2,5 м на горизонтальную плиту, масса которой
2.9.3 Во сколько раз уменьшится энергия нейтрона n при столкновении с ядром углерода C