Тело массой 5 кг покоится на горизонтальной поверхности. К телу приложена сила

Условие задачи:

Тело массой 5 кг покоится на горизонтальной поверхности. К телу приложена сила \(F=10\) Н под углом \(\alpha=60^\circ\) к горизонту. Определите минимальный коэффициент трения, при котором тело останется в покое.

Задача №2.1.47 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=5\) кг, \(F=10\) Н, \(\alpha=60^\circ\), \(\mu_{min }-?\)

Решение задачи:

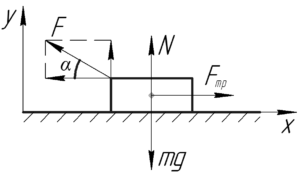На схеме изобразим данное тело, к которому приложены 4 силы: сила тяжести \(mg\), сила реакции опоры \(N\), сила трения покоя \(F_{тр}\) и сила \(F\).

Так как тело покоится, то запишем первый закон Ньютона в проекции на оси координат:

\[\left\{ \begin{gathered}
oy:N + F \cdot \sin \alpha = mg \;\;\;\;(1)\hfill \\
ox:F \cdot \cos \alpha = {F_{тр}} \hfill \;\;\;\;(2)\\
\end{gathered} \right.\]

Внимание! Очень частая ошибка – решающие эту задачу забывают спроецировать силу \(F\) на ось \(y\), в результате чего они получают неправильный ответ.

Сила трения покоя определяется из выражения:

\[{F_{тр}} \leq \mu N\;\;\;\;(3)\]

Из выражения (1) выразим силу нормальной реакции опоры:

\[N = mg – F \cdot \sin \alpha\;\;\;\;(4) \]

Подставим формулы (2) и (4) в выражение (3), в итоге получим:

\[F \cdot \cos \alpha  \leq \mu \left( {mg – F \cdot \sin \alpha } \right)\]

Выражаем искомый коэффициент трения \(\mu\):

\[\mu  \geq \frac{{F \cdot \cos \alpha }}{{mg – F \cdot \sin \alpha }}\]

Минимальное значение этого коэффициента соответствует случаю “равенства”, то есть:

\[{\mu _{min }} = \frac{{F \cdot \cos \alpha }}{{mg – F \cdot \sin \alpha }}\]

Посчитаем численный ответ к этой задаче:

\[{\mu _{\min }} = \frac{{10 \cdot \cos 60^\circ }}{{5 \cdot 10 – 10 \cdot \sin 60^\circ }} = 0,12\]

Ответ: 0,12.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.1.46 Автомобиль идет по горизонтальной дороге со скоростью 72 км/ч. Найти тормозной
2.1.48 Тело, брошенное вертикально вверх с начальной скоростью 30 м/с, достигло высшей
2.1.49 Три бруска, массы которых 0,5, 0,3 и 0,1 кг, связаны нитями и лежат на столе