Решение: Трактор имеет тяговую мощность на крюке, равную 72 кВт. С какой скоростью может

Условие задачи:

Трактор имеет тяговую мощность на крюке, равную 72 кВт. С какой скоростью может тянуть этот трактор прицеп массой 5 т на подъем с углом наклона 11,5° при коэффициенте трения 0,4?

Задача №2.7.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(N=72\) кВт, \(m=5\) т, \(\alpha=11,5^\circ\), \(\mu=0,4\), \(\upsilon-?\)

Решение задачи:

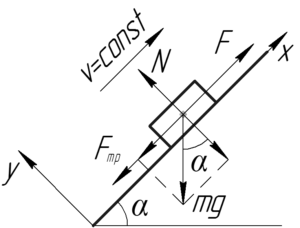Если трактор тянет прицеп равномерно со скоростью \(\upsilon\), то тяговую мощность на крюке можно искать по формуле:

\[N = F \cdot \upsilon \;\;\;\;(1)\]

Запишем первый закон Ньютона в проекции на оси \(x\) и \(y\) (смотрите рисунок):

\[\left\{ \begin{gathered}
ox:F = mg \cdot \sin \alpha + {F_{тр}} \hfill \\
oy:N = mg \cdot \cos \alpha \hfill \\
\end{gathered} \right.\]

Силу трения скольжения находят по формуле (используя нижнее равенство из системы \(N = mg \cdot \cos \alpha\)):

\[{F_{тр}} = \mu N = \mu mg \cdot \cos \alpha \]

Тогда верхнее равенство системы примет такой вид:

\[F = mg \cdot \sin \alpha + \mu mg \cdot \cos \alpha \]

\[F = mg\left( {\sin \alpha + \mu \cos \alpha } \right)\]

Подставим полученное выражение для силы \(F\) в формулу (1):

\[N = mg\left( {\sin \alpha + \mu \cos \alpha } \right) \cdot \upsilon \]

Откуда получим решение задачи:

\[\upsilon = \frac{N}{{mg\left( {\sin \alpha + \mu \cos \alpha } \right)}}\]

Учитывая, что (\(5\;т = 5000\; кг\)), посчитаем ответ:

\[\upsilon = \frac{{72 \cdot {{10}^3}}}{{5000 \cdot 10 \cdot \left( {\sin 11,5^\circ + 0,4 \cdot \cos 11,5^\circ } \right)}} = 2,44\;м/с = 8,77\;км/ч\]