Трактор массой 10 т и мощностью 150 кВт поднимается в гору со скоростью 5 м/с

Условие задачи:

Трактор массой 10 т и мощностью 150 кВт поднимается в гору со скоростью 5 м/с. Найти угол наклона горы к горизонту.

Задача №2.7.46 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=10\) т, \(N=150\) кВт, \(\upsilon=5\) м/с, \(\alpha-?\)

Решение задачи:

Если трактор движется в гору равномерно, то развиваемая им мощность \(N\) равна произведению силы тяги \(F\) на скорость движения \(\upsilon\).

\[N = F \cdot \upsilon \]

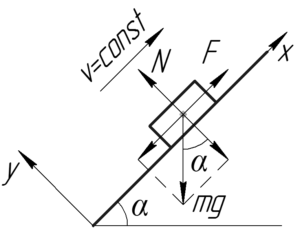
Условно покажем на схеме трактор и все силы, приложенные к нему: это сила тяжести \(mg\), реакция опоры \(N\) и сила тяги \(F\). Так как трактор движется в гору равномерно, то из первого закона Ньютона в проекции на ось \(x\) следует, что:

\[F = mg \cdot \sin \alpha \]

Поэтому:

\[N = mg \cdot \sin \alpha  \cdot \upsilon \]

Выразим искомый угол наклона горы \(\alpha\):

\[\alpha  = \arcsin \left( {\frac{N}{{mg \cdot \upsilon }}} \right)\]

Переведем массу трактора в систему СИ:

\[10\;т = 10000\;кг\]

Посчитаем ответ:

\[\alpha  = \arcsin \left( {\frac{{150 \cdot {{10}^3}}}{{10000 \cdot 10 \cdot 5}}} \right) = 17,5^\circ  = 0,3\;рад\]

Ответ: 0,3 рад.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.7.45 Трактор имеет тяговую мощность на крюке, равную 72 кВт. С какой скоростью может
2.7.47 Ядро массой 8 кг, выпущенное метателем под углом 45 градусов к горизонту с высоты
2.7.48 Допустим, что сила, которая заставляет баржу двигаться по каналу, прямо пропорциональна