Решение: Укажите график зависимости потенциальной энергии свободно падающего тела

Условие задачи:

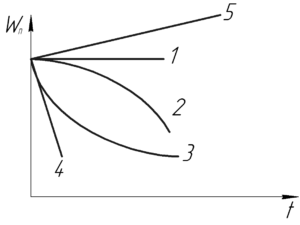Укажите график зависимости потенциальной энергии свободно падающего тела от времени. (Рисунок к задаче приведен справа.)

Задача №2.7.36 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

Обратите внимание, что все приведенные зависимости при \(t=0\) имеют некоторое ненулевое значение, значит отсчет потенциальной энергии ведётся с уровня Земли, и изначально тело находится на некоторой высоте \(H\).

Потенциальную энергию в любой момент времени следует искать по формуле:

\[{W_п} = mgh\]

Здесь \(h\) – высота тела над Землей в момент времени \(t\).

Если тело свободно падает с некоторой высоты \(H\), то его высоту над Землей в любой момент времени можно найти по следующей формуле:

\[h = H – \frac{{g{t^2}}}{2}\]

Тогда:

\[{W_п} = mg\left( {H – \frac{{g{t^2}}}{2}} \right)\]

Раскроем скобки:

\[{W_п} = mgH – \frac{{m{g^2}{t^2}}}{2}\]

Графиком полученной функции является парабола с ветвями, направленными вниз, вершина которой поднята на величину \(mgH\) (на начальную потенциальную энергию). Из всех представленных графиков под заданное описание подходит только график №2.