Решение: В сельском хозяйстве применяются дисковые разбрасыватели удобрений. Какой должна

Условие задачи:

В сельском хозяйстве применяются дисковые разбрасыватели удобрений. Какой должна быть наименьшая частота вращения диска, чтобы удобрение, поступающее на горизонтальный диск в 10 см от оси, разбрасывалось по полю? Коэффициент трения равен 0,9.

Задача №2.4.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=10\) см, \(\mu=0,9\), \(\nu-?\)

Решение задачи:

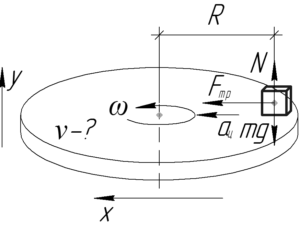На тело (удобрение) действуют следующие силы: сила тяжести \(mg\), сила реакции опоры \(N\) и сила трения скольжения \(F_{тр}\). Первый закон Ньютона в проекции на ось \(y\) даст такое равенство:

\[N = mg\]

Тогда силу трения скольжения можно найти по формуле:

\[{F_{тр}} = \mu N = \mu mg\;\;\;\;(1)\]

Второй закон Ньютона в проекции на ось \(y\) выглядит так:

\[{F_{тр}} = m{a_ц}\]

Чтобы выразить центростремительное ускорение \(a_ц\) через частоту вращения диска, запишем следующие формулы (первая – это формула определения центростремительного ускорения через угловую скорость, вторая – формула связи угловой скорости и частоты вращения):

\[{a_ц} = {\omega ^2}R\]

\[\omega = 2\pi \nu \]

Тогда:

\[{a_ц} = 4{\pi ^2}{\nu ^2}R\]

\[{F_{тр}} = 4{\pi ^2}{\nu ^2}mR\]

Учитывая (1), имеем:

\[4{\pi ^2}{\nu ^2}mR = \mu mg\]

\[\nu = \frac{1}{{2\pi }}\sqrt {\frac{{\mu g}}{R}} \]

Переведем расстояние \(R\) в систему СИ:

\[10\; см = \frac{{10}}{{100}}\; м = 0,1\; м\]

Посчитаем численный ответ:

\[\nu = \frac{1}{{2 \cdot 3,14}}\sqrt {\frac{{0,9 \cdot 10}}{{0,1}}} = 1,51\; Гц = 90,6\; об/мин\]

Более правильным является рассмотрение тела в неинерциальной системе отсчета, связанной с диском. Тогда будет понятно, что при достижении центробежной силы (равной \(\overrightarrow {{F_ц}} = – m\overrightarrow {{a_ц}}\)) величины, равной максимальной силы трения (т.е \({F_{тр.п.макс}} = \mu N\)), тело начнет равномерное движение по диску. Но рассмотрение неинерциальных систем отсчета выходит за рамки школьного курса физики.