icodepro.ruУсловие задачи:
В школьном опыте с “мертвой петлей” шарик массой 0,1 кг отпущен с высоты \(h=3R\). С какой силой шарик давит на опору в верхней точке петли?
Задача №2.8.44 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=0,1\) кг, \(h=3R\), \(P-?\)
Решение задачи:
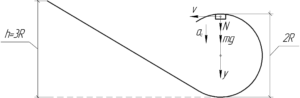Согласно третьему закону Ньютона с какой силой шарик давит на опору, с такой же силой опора давит на шарик. Это означает, что искомая сила давления \(P\) равна силе реакции опоры \(N\).
\[P = N\;\;\;\;(1)\]
На тело в верхней точке петли действуют две силы: сила тяжести и сила реакции опоры. Запишем второй закон Ньютона в проекции на ось \(y\).
\[N + mg = m{a_ц}\]
\[N = m\left( {{a_ц} – g} \right)\]
Центростремительное ускорение равно отношению квадрата скорости шарика в этой точке к радиусу кривизны (петли).
\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\]
\[N = m\left( {\frac{{{\upsilon ^2}}}{R} – g} \right)\;\;\;\;(2)\]
Так как сила трения отсутствует, то по закону сохранения энергии полная механическая энергия шарика сохраняется. Значит начальная потенциальная энергия шарика преобразуется в верхней точке петли в кинетическую и потенциальную энергии.
\[mgh = \frac{{m{\upsilon ^2}}}{2} + mg \cdot 2R\]
По условию \(h=3R\), поэтому:
\[mg \cdot 3R = \frac{{m{\upsilon ^2}}}{2} + mg \cdot 2R\]
\[gR = \frac{{{\upsilon ^2}}}{2}\]
\[{\upsilon ^2} = 2gR\;\;\;\;(3)\]
Подставим выражение (3) в (2), тогда:
\[N = m\left( {\frac{{2gR}}{R} – g} \right)\]
\[N = mg\]
Согласно равенству (1) следует:
\[P = mg\]
Посчитаем численный ответ к задаче:
\[P = 0,1 \cdot 10 = 1\; Н\]
Ответ: 1 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.43 Тело скользит вниз по наклонной плоскости, плавно переходящей в вертикальную
2.8.45 Вертикальный невесомый стержень длиной 6 м подвешен одним концом к оси
2.8.46 Колодец, имеющий глубину 5 м, площадь дна 0,5 м2, наполовину заполнен водой
