icodepro.ruУсловие задачи:
Вагон массой 50 т движется со скоростью 12 км/ч и встречает стоящую на пути платформу массой 30 т. Найти расстояние, пройденное вагоном и платформой после сцепления, если сила сопротивления составляет 5% от веса.
Задача №2.10.18 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(M=50\) т, \(\upsilon_0=12\) км/ч, \(m=30\) т, \(\alpha=5\)%, \(S-?\)
Решение задачи:
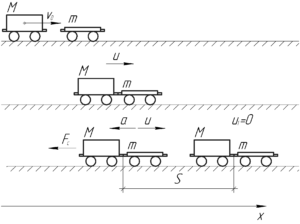Применим закон сохранения импульса в проекции на горизонтальную ось:
\[M{\upsilon _0} = \left( {m + M} \right)u\]
\[u = \frac{{M{\upsilon _0}}}{{m + M}}\;\;\;\;(1)\]
Отлично, мы нашли скорость вагона и платформы сразу после сцепления. Далее они начнут равнозамедленное движения из-за действия на них силы сопротивления. Запишем второй закон Ньютона в проекции на ось \(x\):
\[ – {F_с} = – \left( {m + M} \right)a\]
\[{F_с} = \left( {m + M} \right)a\]
Согласно условию сила сопротивления равна:
\[{F_с} = \alpha \left( {m + M} \right)g\]
Значит:
\[\alpha \left( {m + M} \right)g = \left( {m + M} \right)a\]
\[a = \alpha g\;\;\;\;(2)\]
Из курса кинематики известно, что разность квадратов конечной и начальной скорости равно удвоенному произведению ускорения на пройденное расстояние со знаком минус (он присутствует здесь, так как движение замедленное).
\[0 – {u^2} = – 2aS\]
\[S = \frac{{{u^2}}}{{2a}}\]
Учитывая ранее найденные выражения (1) и (2), получим такое решение этой задачи в общем виде:
\[S = \frac{{{M^2}\upsilon _0^2}}{{2\alpha g{{\left( {m + M} \right)}^2}}}\]
Переведем массы вагона и платформы, а также скорость вагона в систему СИ:
\[50\; т = 50 \cdot {10^3}\; кг = 5 \cdot {10^4}\; кг\]
\[30\; т = 30 \cdot {10^3}\; кг = 3 \cdot {10^4}\; кг\]
\[12\; км/ч = \frac{{12 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{120}}{{36}}\; м/с = \frac{{10}}{3}\; м/с\]
Посчитаем ответ:
\[S = \frac{{{{\left( {5 \cdot {{10}^4}} \right)}^2} \cdot {{10}^2}}}{{{3^2} \cdot 2 \cdot 0,05 \cdot 10 \cdot {{\left( {3 \cdot {{10}^4} + 5 \cdot {{10}^4}} \right)}^2}}} = 4,34\; м = 434\; см\]
Ответ: 434 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.17 Два мальчика играют в мяч, стоя на льду на расстоянии 10 м друг от друга
2.10.19 Конькобежец, стоя на льду, бросает горизонтально с высоты 1,5 м груз массой 10 кг
2.10.20 Кусок пластилина массой m=32 г попадает в брусок массой 6m, двигавшийся
Откуда в вычислениях в знаменателе 3 в квадрате?
Это 10/3 в квадрате
Здесь важно отметить, что при сцеплении механическая энергия не сохраняется. Можно рассчитать потерянную часть энергии
По какой формуле можно рассчитать потерянную часть энергии?
Нужно воспользоваться законом сохранения энергии
Верно, механическая энергия не сохраняется
Я не понимаю, разве тут можно использовать формулу с обозначением “g”? Ведь “g=10” – применимо только при свободном падении объекта. Можете пояснить почему мы имеем право использовать данное обозначение в нашем случае про вагон с платформой?
Сила тяжести любого тела на Земле определяется по формуле:\[{F_т} = mg\]Если тело падает свободно, то есть под действием только одной силы – силы тяжести – то второй закон Ньютона для этого тела запишется в виде:\[{F_т} = ma\]Учитывая верхнюю формулу, получим:\[ma = mg\]\[a = g\]В кинематике не рассматриваются вопросы о том, что вызвало соответствующее ускорение тела (то есть какая сила), поэтому учащимся кажется, что \(g\) появилось само собой в кинематике.
Я Вам показал, откуда оно взялось – из формулы для силы тяжести. Думать, что ускорение свободного падения \(g\) используется только в случае свободного падения – неверно, оно используется практически в любой задаче по динамике, поскольку является по сути коэффициентом, который показывает с какой силой Земля действует на тело единичной массы.