Решение: Вертикальный невесомый стержень длиной 6 м подвешен одним концом к оси

Условие задачи:

Вертикальный невесомый стержень длиной 6 м подвешен одним концом к оси вращения. На другом конце и посередине стержня закреплены две равные точечные массы. Какую минимальную скорость нужно сообщить нижнему концу стержня, чтобы он отклонился в горизонтальное положение?

Задача №2.8.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(L=6\) м, \(\upsilon_1-?\)

Решение задачи:

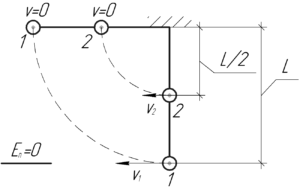Так как две точечные массы связаны между собой стержнем, то при сообщении скорости нижней массе скорость появится и у той, которая находится посередине. Так как стержень жесткий, то у этих масс при дальнейшем движении в каждый момент времени будет одинаковая угловая скорость \(\omega\). Учитывая, что расстояние от нижней массы до оси вращения равно \(L\), а от массы, находящейся посередине – \(\frac{L}{2}\), справедливо записать:

\[\left\{ \begin{gathered}
{\upsilon _1} = \omega L \hfill \\
{\upsilon _2} = \omega \frac{L}{2} \hfill \\
\end{gathered} \right.\]

Поделим нижнее выражение системы на верхнее, так мы найдем как соотносят скорости этих тел.

\[\frac{{{\upsilon _2}}}{{{\upsilon _1}}} = \frac{1}{2} \Rightarrow {\upsilon _2} = \frac{{{\upsilon _1}}}{2}\;\;\;\;(1)\]

Поскольку сила реакции в точке соединения стержня с шарниром работы не совершает, то по закону сохранения энергии полная механическая энергия системы должна сохраняться. Уровень нуля потенциальной энергии выберем на уровне начального положения нижнего тела.

В начале (то есть после сообщения скоростей обеим массам) у тел имеется кинетическая энергия, а у массы посередине – ещё и потенциальная. В конце у обоих тел будет иметься только потенциальная энергия.

\[\frac{{m\upsilon _1^2}}{2} + \frac{{m\upsilon _2^2}}{2} + mg\frac{L}{2} = 2mgL\]

Учитывая (1), имеем:

\[\frac{{m\upsilon _1^2}}{2} + \frac{{m\upsilon _1^2}}{8} + mg\frac{L}{2} = 2mgL\]

\[\frac{{5m\upsilon _1^2}}{8} = mg\frac{{3L}}{2}\]

\[{\upsilon _1} = \sqrt {\frac{{12gL}}{5}} \]

Осталось только посчитать ответ.

\[{\upsilon _1} = \sqrt {\frac{{12 \cdot 10 \cdot 6}}{5}} = 12\; м/с = 43,2\; км/ч\]