Условие задачи:

Два чайника, каждый из которых потребляет при напряжении 200 В по 400 Вт, закипают при последовательном и параллельном включении за одно и то же время. Каково сопротивление подводящих проводов?

Задача №7.4.52 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(U_0=200\) В, \(P_0=400\) Вт, \(t_1=t_2\), \(R-?\)

Решение задачи:

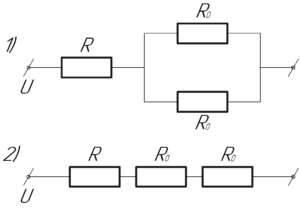Если чайники, нагревая одно и то же количество воды, закипают за одно и то же время, значит в них выделяется одна и та же мощность, то есть:

\[{P_1} = {P_2}\;\;\;\;(1)\]

Сначала определим сопротивление чайников \(R_0\). Так как при напряжении \(U_0\) они потребляют мощность \(P_0\), то сопротивление \(R_0\) найдем следующим образом:

\[{P_0} = \frac{{U_0^2}}{{{R_0}}} \Rightarrow {R_0} = \frac{{U_0^2}}{{{P_0}}}\;\;\;\;(2)\]

Найдем мощность \(P_1\), выделяющуюся в каждом чайнике при их последовательном соединении. Пусть напряжение сети, к которым подключены чайники, равно \(U\). Тогда через чайники будет течь ток \(I_1\), который можно определить по закону Ома:

\[{I_1} = \frac{U}{{R + 2{R_0}}}\]

Тогда мощность \(P_1\) равна:

\[{P_1} = I_1^2{R_0}\]

\[{P_1} = \frac{{{U^2}{R_0}}}{{{{\left( {R + 2{R_0}} \right)}^2}}}\]

Далее определим мощность \(P_2\), выделяющуюся в каждом чайнике при их параллельном соединении. Через соединительные провода будет течь ток \(I_2\), который также определим из закона Ома:

\[{I_2} = \frac{U}{{R + 0,5{R_0}}}\]

Так как чайники одинаковые (то есть имеют одинаковые сопротивления), то через них течет ток \(\frac{I_2}{2}\). Тогда мощность \(P_2\) равна:

\[{P_2} = {\left( {\frac{{{I_2}}}{2}} \right)^2}{R_0} = \frac{1}{4}I_2^2{R_0}\]

\[{P_2} = \frac{{{U^2}{R_0}}}{{4{{\left( {R + 0,5{R_0}} \right)}^2}}}\]

Учитывая (1), имеем:

\[\frac{{{U^2}{R_0}}}{{{{\left( {R + 2{R_0}} \right)}^2}}} = \frac{{{U^2}{R_0}}}{{4{{\left( {R + 0,5{R_0}} \right)}^2}}}\]

\[{\left( {R + 2{R_0}} \right)^2} = 4{\left( {R + 0,5{R_0}} \right)^2}\]

Раскроем скобки в обеих частях уравнения:

\[{R^2} + 4R{R_0} + 4R_0^2 = 4{R^2} + 4R{R_0} + R_0^2\]

\[{R^2} + 4R_0^2 = 4{R^2} + R_0^2\]

\[3{R^2} = 3R_0^2\]

\[R = {R_0}\]

Принимая во внимание (2), получим:

\[R = \frac{{U_0^2}}{{{P_0}}}\]

Численный ответ задачи равен:

\[R = \frac{{{{200}^2}}}{{400}} = 100\;Ом = 0,1\;кОм\]

Ответ: 0,1 кОм.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

7.4.51 Найти ток короткого замыкания в цепи генератора с ЭДС 70 В, если при увеличении
7.4.53 При силе тока 2 А во внешней цепи выделяется мощность 24 Вт, а при силе тока 5 А — мощность 30 Вт
7.4.54 Элемент замыкают один раз сопротивлением 4 Ом, другой — резистором сопротивлением 9 Ом