Условие задачи:
Два элемента соединены параллельно. Один имеет ЭДС \(\rm E_1=2\) В и внутреннее сопротивление \(r_1=0,3\) Ом, другой \(\rm E_2=1,5\) В и \(r_2=0,2\) Ом. Определить напряжение на зажимах элементов. Сопротивлением соединительных проводов пренебречь.
Задача №7.2.32 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\rm E_1=2\) В, \(r_1=0,3\) Ом, \(\rm E_2=1,5\) В, \(r_2=0,2\) Ом, \(U-?\)
Решение задачи:
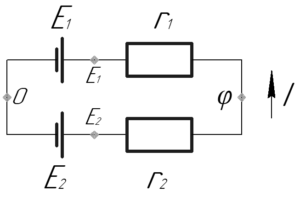 Сначала нарисуем схему для решения этой задачи, на которой в характерных точках расставим потенциалы, при этом внутренние сопротивления источников покажем отдельно (смотрите схему, представленную справа, на ней хорошо видны эти точки). Очевидно, что искомое напряжение на зажимах элементов \(U\) будет равно:
Сначала нарисуем схему для решения этой задачи, на которой в характерных точках расставим потенциалы, при этом внутренние сопротивления источников покажем отдельно (смотрите схему, представленную справа, на ней хорошо видны эти точки). Очевидно, что искомое напряжение на зажимах элементов \(U\) будет равно:
\[U = \varphi — 0\]
\[U = \varphi \;\;\;\;(1)\]
Пусть ток в цепи \(I\) течет против часовой стрелки (смотрите схему). Запишем дважды закон Ома для определения токов, текущих через сопротивления \(r_1\) и \(r_2\) (а этот ток, очевидно, одинаковый):
\[\left\{ \begin{gathered}
I = \frac{{{{\rm E}_2} — \varphi }}{{{r_2}}} \hfill \\
I = \frac{{\varphi — {{\rm E}_1}}}{{{r_1}}} \hfill \\
\end{gathered} \right.\]
То есть мы имеем такое равенство:
\[\frac{{{{\rm E}_2} — \varphi }}{{{r_2}}} = \frac{{\varphi — {{\rm E}_1}}}{{{r_1}}}\]
Перемножим «крест-накрест»:
\[{r_1}\left( {{{\rm E}_2} — \varphi } \right) = {r_2}\left( {\varphi — {{\rm E}_1}} \right)\]
Раскроем скобки в обеих частях уравнения:
\[{{\rm E}_2}{r_1} — \varphi {r_1} = \varphi {r_2} — {{\rm E}_1}{r_2}\]
В правую часть перенесем все члены с \(\varphi\), далее вынесем его за скобки, остальные — в левую часть:
\[{{\text{E}}_1}{r_2} + {{\text{E}}_2}{r_1} = \varphi \left( {{r_1} + {r_2}} \right)\]
\[\varphi = \frac{{{{\text{E}}_1}{r_2} + {{\text{E}}_2}{r_1}}}{{{r_1} + {r_2}}}\]
Учитывая (1), окончательно имеем:
\[U = \frac{{{{\text{E}}_1}{r_2} + {{\text{E}}_2}{r_1}}}{{{r_1} + {r_2}}}\]
Мы получили решение задачи в общем виде, давайте посчитаем ответ:
\[U = \frac{{2 \cdot 0,2 + 1,5 \cdot 0,3}}{{0,3 + 0,2}} = 1,7\;В\]
Хотим заметить, что это не единственное решение этой задачи. Дело в том, что элементы могут быть подключены разноименными полюсами, тогда ответ будет иным. Ответ на вопрос «каким?» оставим для пытливых читателей. Но сразу обнадежим — задача будет решаться аналогично, правда нужно правильно расставить потенциалы тех же точек.
Ответ: 1,7 В.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.2.31 Два элемента с внутренним сопротивлением 0,2 и 0,4 Ом соединены одинаковыми полюсами
7.2.33 Два элемента с ЭДС, равными E1=1,5 В и E2=2 В, соединены одинаковыми полюсами
7.2.34 Определить число последовательно соединенных элементов с ЭДС 1,2 В и внутренним

 icodepro.ru
icodepro.ru
Пожалуйста объясните почему закон Ома записывается так.
В данном случае я записал закон Ома для участка цепи, согласно которому сила тока прямо пропорциональна напряжению (разности потенциалов) и обратно пропорциональна сопротивлению, то есть:\[I = \frac{\Delta \varphi}{R}\]Потенциал некоторой точки я принял равным нулю, а потенциал остальных я расставил, руководствуясь некоторыми правилами. Например, ЭДС увеличивает потенциал на величину ЭДС (простите за «масло масляное»). Неизвестный потенциал точки между резисторами я обозначил за \(\varphi\).