Условие задачи:
Два маленьких одинаковых металлических шарика заряжены положительным зарядом \(5q\) и отрицательным зарядом \(-q\) и находятся на некотором расстоянии друг от друга в вакууме. Шарики привели в соприкосновение и развели на прежнее расстояние, поместив их в жидкий диэлектрик с диэлектрической проницаемостью \(\varepsilon = 2\). Найти изменение модуля силы взаимодействия шариков?
Задача №6.1.31 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(5q\), \(-q\), \(\varepsilon = 2\), \(\frac{F_0}{F}-?\)
Решение задачи:
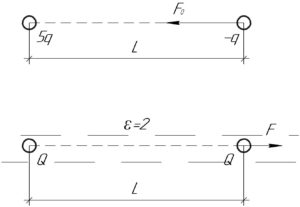 Модуль начальной силы электрического взаимодействия шариков \(F_0\) вследствие притяжения зарядов \(5q\) и \(-q\) согласно закону Кулона равен:
Модуль начальной силы электрического взаимодействия шариков \(F_0\) вследствие притяжения зарядов \(5q\) и \(-q\) согласно закону Кулона равен:
\[F = \frac{{5k{q^2}}}{{{L^2}}}\]
Заряды приводят в соприкосновение, теперь на каждом из шариков окажется заряд \(Q\), определяемый таким образом:
\[Q = \frac{{5q + \left( { — q} \right)}}{2} = 2q\;\;\;\;(1)\]
Когда заряды поместят в диэлектрик с диэлектрической проницаемостью \(\varepsilon\), то они будут отталкиваться с силой \(F\), модуль которой согласно закону Кулона равен:
\[F = \frac{{k{Q^2}}}{{\varepsilon {L^2}}}\]
Учитывая равенство (1) и то, что \(\varepsilon = 2\), имеем:
\[F = \frac{{4k{q^2}}}{{2{L^2}}}\]
\[F = \frac{{2k{q^2}}}{{{L^2}}}\]
В итоге получим:
\[\frac{{{F_0}}}{F} = \frac{{5k{q^2} \cdot {L^2}}}{{{L^2} \cdot 2k{q^2}}} = 2,5\]
Ответ: уменьшится в 2,5 раза.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.1.30 Точечные положительные заряды q и 2q закреплены на расстоянии L друг
6.2.1 Указать размерность единицы напряженности электростатического поля
6.2.2 Определить напряженность электрического поля, если на точечный заряд 1 мкКл

 icodepro.ru
icodepro.ru
А разве изменение не стоит обозначить как дельта и искать разность?
Автор неясно сформулировал вопрос задачи. Я всё же склоняюсь к тому, что здесь нужно найти относительное изменение, а не абсолютное.
Но хороший учитель примет и ваше решение, где Вы найдете абсолютное изменение
почему в первой формуле у нас получается без минуса ? мы берем по модулю заряды или как ?
Да, заряды берем по модулю, чтобы найти модуль силы электрического взаимодействия